题目内容
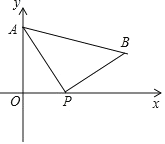
【题目】平面直角坐标系xOy中,点A、B分别在函数y1=![]() (x>0),与y2=﹣
(x>0),与y2=﹣![]() (x<0)的图象上,A、B的横坐标分别为a、b.(a、b为任意实数)
(x<0)的图象上,A、B的横坐标分别为a、b.(a、b为任意实数)
(1)若AB∥x轴,求△OAB的面积;
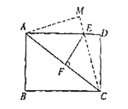
(2)作边长为2的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,当a≥3时,CD边与函数y1=![]() (x>0)的图象有交点,请说明理由.
(x>0)的图象有交点,请说明理由.
【答案】(1)3;(2)见解析.
【解析】
(1)点A、B的坐标分别为(a,![]() )、(b,﹣
)、(b,﹣![]() ),AB∥x轴,则
),AB∥x轴,则![]() ,即可求解;
,即可求解;
(2)设点A(a,![]() ),则点C(a﹣2,
),则点C(a﹣2,![]() ),点D(a﹣2,
),点D(a﹣2,![]() ),点F(a﹣2,
),点F(a﹣2,![]() ),验证2﹣FC≥0,即可求解
),验证2﹣FC≥0,即可求解
解:(1)A、B的横坐标分别为a、b,
则点A、B的坐标分别为(a,![]() )、(b,﹣
)、(b,﹣![]() ),
),
AB∥x轴,则![]() ,
,
则a=﹣b,AB=a﹣b=2a,
S△OAB=![]() ×2a×
×2a×![]() =3;
=3;
(2)如图所示:
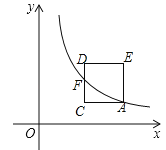
∵a≥3,AC=2,则直线CD在y轴右侧且平行于y轴,CD与函数图象有交点,设交点为F,
设点A(a,![]() ),则点C(a﹣2,
),则点C(a﹣2,![]() ),点D(a﹣2,
),点D(a﹣2,![]() ),点F(a﹣2,
),点F(a﹣2,![]() )
)
则2﹣FC=2﹣![]() +
+![]() =
=![]() ,
,
∵a≥3,∴a﹣3≥0,a﹣2>0,
故2﹣FC≥0,FC≤2,
即点F在线段CD上,
即当a≥3时,CD边与函数y1=![]() (x>0)的图象有交点.
(x>0)的图象有交点.

练习册系列答案
相关题目