题目内容
【题目】已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=8,O是AB边的中点,P是AC边上的动点,OE⊥OP交BC边于点E,连接PE.
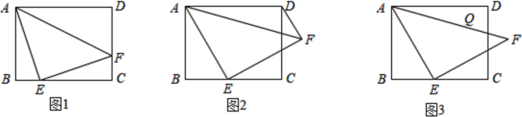
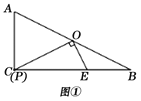
(1)如图①,当P与C重合时,线段PE的长为___________;
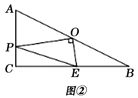
(2)如图②,当P在AC边上运动时,
①探究:线段PA,PE,EB之间的数量关系,并证明你的结论;
②若设PA=![]() ,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
【答案】(1)5;(2)①PA2+EB2=PE2,证明见解析.②y=![]() x25x+25 2
x25x+25 2![]()
【解析】分析:(1)根据中线定理和直角三角形斜边上的中线分别表示出AB、OA的长度,再证明△COE∽△BCD即可.
(2)①如下图②,先判断△BOM≌△AOP,可得:BM2+EB2=ME2,又∵OE⊥PM,OM=OP,∴ME=PE,即可证明BM2+EB2=ME2.
②求出y与x之间的函数关系式即可解答.
详解:(1)在Rt△ABC中,AB=![]() ,
,
∵O是AB中点,∴OA=CO=BO=![]() AB=2
AB=2![]() .
.
∴∠OCB=∠B,又∵OE⊥OP,∴∠COE=∠A=90°.
∴△COE∽△BCD,
∴![]() ,即:
,即:![]() ,∴CE=5.
,∴CE=5.
(2)①三者的数量关系为PA2+EB2=PE2.
证明:如图②,延长PO到M,使OM=OP,连接BM,EM,

∵O是AB边的中点,∴0B=OA,
又 ∠BOM=∠AOP,∴△BOM≌△AOP,
∴∠OBM=∠OAP,BM=AP.
∴∠OBM+∠ABC=∠BAC+∠ABC=90°,
∴BM2+EB2=ME2,
又∵OE⊥PM,OM=OP,∴ME=PE,
∴PA2+EB2=PE2.
②如图②,设EB=m,则CE=8-m,∵ PA=x,则PC=4-x,又PE2=y,
在Rt△PEC中,由勾股定理得:PC2+CE2=PE2,
则(4-x)2+(8-m)2=y ①.
又PA2+EB2=PE2,则x2+m2=y,②.
由①②联解消y得:m=-![]() ③,
③,
将③代入②并整理,得:y=![]() ,
,
∴y与x之间的函数关系式为![]() ,
,
∵![]() =
=![]() ,
,
∴当x=2时,y的最小值为20,∴PE的最小值为2![]() .
.

 阅读快车系列答案
阅读快车系列答案