题目内容
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿着对角线
沿着对角线![]() 对折得到
对折得到![]() .
.
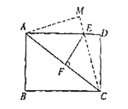
(1)如图,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
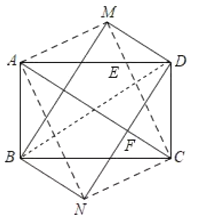
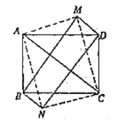
(2)如图,再将![]() 沿着对角线
沿着对角线![]() 对折得到
对折得到![]() ,顺次连接
,顺次连接![]() 、
、![]() 、
、![]() 、
、![]() ,求:四边形
,求:四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() 的面积是
的面积是![]() .
.
【解析】
(1)由矩形的性质可得AB=CD=3,AD=BC=4,∠B=∠D=90°,AD∥BC,由勾股定理可求AC=5,由折叠的性质和平行线的性质可得AE=CE,由勾股定理可求AE的长,由三角形面积公式可求EF的长;
(2)由折叠的性质可得AB=AM=3,CD=CN=3,∠BAC=∠CAM,∠ACD=∠ACN,AC⊥DN,DF=FN,由“SAS”可证△BAM≌△DCN,△AMD≌△CNB可得
MD=BN,BM=DN,可得四边形MDNB是平行四边形,通过证明四边形MDNB是矩形,可得∠BND=90°,由三角形面积公式可求DF的长,由勾股定理可求BN的长,即可求四边形BMDN的面积.
解:(1)∵四边形ABCD是矩形
∴AB=CD=3,AD=BC=4,∠B=∠D=90°,AD∥BC
∴AC=![]() =5,
=5,
∵将Rt△ABC沿着对角线AC对折得到△AMC.
∴∠BCA=∠ACE,
∵AD∥BC
∴∠DAC=∠BCA
∴∠EAC=∠ECA
∴AE=EC
∵EC2=ED2+CD2,
∴AE2=(4AE)2+9,
∴AE=![]() ,
,
∵S△AEC=![]() ×AE×DC=
×AE×DC=![]() ×AC×EF,
×AC×EF,
∴![]() ×3=5×EF,
×3=5×EF,
∴EF=![]() ;
;
(2)如图所示:
∵将Rt△ABC沿着对角线AC对折得到△AMC,将Rt△ADC沿着对角线AC对折得到△ANC,
∴AB=AM=3,CD=CN=3,∠BAC=∠CAM,∠ACD=∠ACN,AC⊥DN,DF=FN,
∵AB∥CD
∴∠BAC=∠ACD
∴∠BAC=∠ACD=∠CAM=∠ACN
∴∠BAM=∠DCN,且BA=AM=CD=CN
∴△BAM≌△DCN(SAS)
∴BM=DN
∵∠BAM=∠DCN
∴∠BAM90°=∠DCN90°
∴∠MAD=∠BCN,且AD=BC,AM=CN
∴△AMD≌△CNB(SAS)
∴MD=BN,且BM=DN
∴四边形MDNB是平行四边形
连接BD,
由1)可知:∠EAC=∠ECA,
∵∠AMC=∠ADC=90°
∴点A,点C,点D,点M四点共圆,
∴∠ADM=∠ACM,
∴∠ADM=∠CAD
∴AC∥MD,且AC⊥DN
∴MD⊥DN,
∴四边形BNDM是矩形
∴∠BND=90°
∵S△ADC=![]() ×AD×CD=
×AD×CD=![]() ×AC×DF
×AC×DF
∴DF=![]()
∴DN=![]()
∵四边形ABCD是矩形
∴AC=BD=5,
∴BN=![]()
∴四边形BMDN的面积=BN×DN=![]() ×
×![]() =
=![]() .
.