题目内容
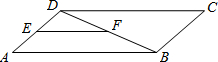如图，在平行四边形ABCD中，EF∥AB，DE：EA=2：3，EF=3，则CD的长是（ ）分析：根据相似三角形的判定和相似三角形的性质以及平行四边形的性质和即可求出CD的长．
解答：解：∵EF∥AB，
∴△DEF∽DAB，
∴
=
，
∵DE：EA=2：3，
∴
=
=
，
∵EF=3，
∴AB=7.5
∵四边形ABCD是平行四边形，
∴CD=AB=7.5．
故选B．
∴△DEF∽DAB，
∴
| DE |
| AD |
| EF |
| AB |
∵DE：EA=2：3，
∴
| DE |
| AD |
| EF |
| AB |
| 2 |
| 5 |
∵EF=3，
∴AB=7.5
∵四边形ABCD是平行四边形，
∴CD=AB=7.5．
故选B．
点评：本题综合性的考查了似三角形的判定和相似三角形的性质以及平行四边形的性质，准确掌握三角形相似判定方法和性质以及平行四边形的性质是解题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
17、如图，在平行四边形ABCD中，EF∥AD，GH∥AB，EF、GH相交于点O，则图中共有
如图，在平行四边形ABCD中，∠ABC的平分线交CD于点E，∠ADC的平分线交AB于点F，证明：四边形DFBE是平行四边形．
的延长线交于点P，FP交AD于点Q．设运动时间为x秒，线段PC的长为y厘米．
如图，在平行四边形ABCD中，AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
（2013•同安区一模）如图，在平行四边形ABCD中，已知∠ODA=90°，AC=10cm，BD=6cm，则AD的长为