题目内容
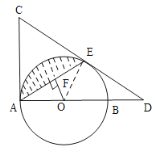
【题目】如图,AB是⊙O的直径,AC⊥AB,E为⊙O上的一点,AC=EC,延长CE交AB的延长线于点D.

(1)求证:CE为⊙O的切线;
(2)若OF⊥AE,OF=1,∠OAF=30°,求图中阴影部分的面积.(结果保留π)
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)首先连接OE,由AC⊥AB,,可得∠CAD=90°,又由AC=EC,OA=OE,易证得∠CAE=∠CEA, ∠FAO=∠FEO,即可证得CD为⊙O的切线;
(2)根据题意可知∠OAF=30°,OF=1,可求得AE的长,又由S阴影=![]() -
-![]() ,即可求得答案.
,即可求得答案.
(1)证明:连接OE
∵AC=EC,OA=OE
∴∠CAE=∠CEA, ∠FAO=∠FEO
∵AC⊥AB,
∴∠CAD=90°
∴∠CAE+∠EAO=90°
∴∠CEA+∠AEO=90°
即∠CEA=90°
∴OE⊥CD
∴CE为⊙O的切线
(2)解:
∵∠OAF=30°,OF=1
∴AO=2
∴AF=![]() 即AE=
即AE=![]()
∴![]()
∵∠AOE= 120°,AO=2
∴![]()
∴S阴影=![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目