题目内容
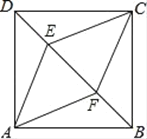
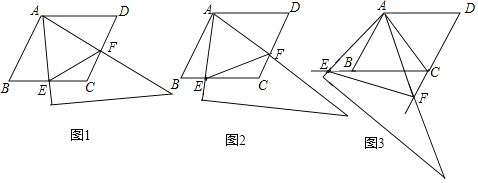
【题目】如图，在正方形
中，
、
分别是
、
边上的点，且
.
（1）求证:
；
（2）若
，
，求
的长.
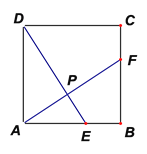
【答案】（1）证明见解析（2）
【解析】分析：(1)根据正方形的性质，用SAS证明△AED≌△BFA，得到∠ADE＝∠BAF，再证∠BAF＋∠AED＝90°；(2)根据∠ADE＝∠BAF，∠AED＝∠PEA，证得△ADE∽△PAE，由对应边成比例求解.
详解：(1)∵四边形ABCD是正方形，∴AD＝AB＝BC，∠DAB＝∠ABC＝90°，
∵E，F分别是AB，BC的中点，∴AE＝BF，
∴△AED≌△BFA(SAS)，∴∠ADE＝∠BAF，
∵∠ADE＋∠AED＝90°，∴∠BAF＋∠AED＝90°，
∴∠APE＝90°，即AF⊥DE.
(2)Rt△ADE中，AD＝4，AE＝3，
由勾股定理得，DE＝5.
∵∠ADE＝∠BAF，∠AED＝∠PEA，
∴△ADE∽△PAE，∴AE2＝EP·ED.
∴32＝5EP，EP＝
.
练习册系列答案
相关题目
【题目】为了鼓励市民节约用水，某市水费实行分段计费制，每户每月用水量在规定用量及以下的部分收费标准相同，超出规定用量的部分收费标准相同.下表是小明家1至4月份水量和缴纳水费情况，根据表格提供的数据，回答：
月份 | 一 | 二 | 三 | 四 |
用水量（吨） | 7 | 9 | 12 | 15 |
水费（元） | 14 | 18 | 26 | 35 |
（1）规定用量内的收费标准是 元/吨，超过部分的收费标准是 元/吨；
（2）问该市每户每月用水规定量是多少吨？
（3）若小明家六月份应缴水费50元，则六月份他们家的用水量是多少吨？
