题目内容
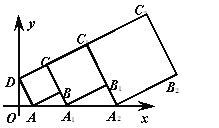
【题目】在平面坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为( )
A. 5·![]() B. 5·
B. 5·![]() C. 5·
C. 5·![]() D. 5·
D. 5·![]()
【答案】D
【解析】分析: 先求出正方形ABCD的边长和面积,再求出第一个正方形A1B1C1C的面积,得出规律,根据规律即可求出正方形A2018B2018C2018C2017的面积.
详解: ∵点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,
∵∠AOD=90°,
∴AB=AD=![]() ,∠ODA+∠OAD=90°,
,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,S正方形ABCD=(![]() )2=5,
)2=5,
∴∠ABA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴![]() =
=![]() ,即
,即 ![]() =
=![]() ,
,
∴BA1=![]() ,
,
∴CA1=![]() ,
,
∴正方形A1B1C1C的面积=(![]() )2=5×
)2=5×![]() ,…,
,…,
故正方形A2018B2018C2018C2017的面积为:5×(![]() )2018=5·
)2018=5·![]() .
.
故选:D.
点睛: 本题考查了正方形的性质以及坐标与图形性质;通过求出正方形ABCD和正方形A1B1C1C的面积得出规律是解决问题的关键.

 小学课时特训系列答案
小学课时特训系列答案【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.