题目内容
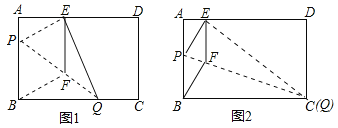
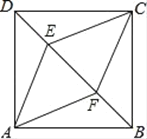
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
【答案】(1)四边形AECF是菱形,理由见解析;(2)四边形AECF的周长为![]() .
.
【解析】
(1)首先连接AC,交BD于点O,根据正方形的性质,可得AC⊥BD,OA=OC=OB=OD,又由DE=BF,得出OE=OF,对角线互相垂直平分,进而可判定四边形AECF是菱形;
(2)由已知条件可得,AC=BD=8,根据勾股定理,得出AE,进而可得出四边形AECF的周长.
(1)四边形AECF是菱形,理由如下:
连接AC,交BD于点O,如图所示,
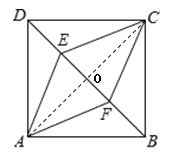
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD
∵DE=BF
∴OE=OF
∴四边形AECF是菱形(对角线互相垂直且平分的四边形是菱形);
(2)∵EF=4,DE=BF=2,
∴AC=BD=8,
∴AE=OA2+OE2=![]() ,
,
∴四边形AECF的周长为![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】某区选取了10名同学参加兴隆台区“汉字听取大赛”,他们的年龄(单位:岁)记录如下:
年龄(单位:岁) | 13 | 14 | 15 | 16 | 17 |
人数 | 2 | 2 | 3 | 2 | 1 |
这些同学年龄的众数和中位数分别是( )
A.15,15B.15,16C.3,3D.3,15