题目内容
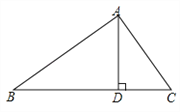
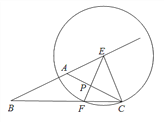
【题目】如图，己知在△ABC中，AB=AC，tanB=
，BC =4，点E是在线段BA延长线上一点，以点E为圆心，EC为半径的圆交射线BC于点C、F（点C、F不重合），射线EF与射线AC交于点P.
（1）求证：AE2=AP·AC；
（2）当点F在线段BC上，设CF=x，△PFC的面积为y，求y关于x的函数解析式及定义域；
（3）当
时，求BE的长.
【答案】（1）证明见解析（2）
（3）
或
【解析】分析：
证明
根据相似三角形对应边成比例即可证明.
证明
根据相似三角形的性质得到，
.
.代入即可.
分两种情况进行讨论：①当点F在线段BC上时，②当点F在线段BC的延长线上时，
分别求解即可.
详解：（1）∵
∴
∵
∴
∵
又∵
∴
∵
是公共角，
∴
∴
∴
.
（2）∵
∴
∴.
过点
作
于点
∵
经过圆心，
∴
.∴
.
在
中，∵
∴
.
∴.
∴
.
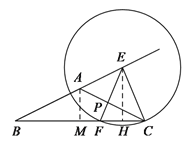
（3） ①当点F在线段BC上时，
∵
∴
∵△AEP∽△ACE.
∴
∴
.
过点
作
垂足为点
∵ 
∴
中，∵
∴
∴
∴.
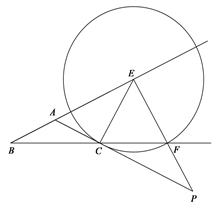
②当点F在线段BC的延长线上时，
∵∠EFC=∠ECF，
.
又∵
∴
∴
∵是公共角，
∴
，∴
∵∴
∴
.
∴
.
综上所述,
或.
练习册系列答案
相关题目
【题目】某区选取了10名同学参加兴隆台区“汉字听取大赛”，他们的年龄(单位：岁)记录如下：
年龄(单位：岁) | 13 | 14 | 15 | 16 | 17 |
人数 | 2 | 2 | 3 | 2 | 1 |
这些同学年龄的众数和中位数分别是( )
A.15，15B.15，16C.3，3D.3，15
