ΧβΡΩΡΎ»ί
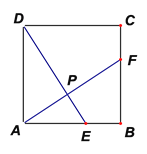
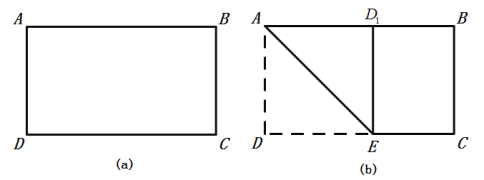
ΓΨΧβΡΩΓΩ“―÷ΣΘΚΥΡ±Ώ–ΈABCD «Νβ–ΈΘ§ABΘΫ4Θ§ΓœABCΘΫ60ΓψΘ§”–“ΜΉψΙΜ¥σΒΡΚ§60ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«≥ΏΒΡ60ΓψΫ«ΒΡΕΞΒψ”κΝβ–ΈABCDΒΡΕΞΒψA÷ΊΚœΘ§ΝΫ±ΏΖ÷±π…δœΏCBΓΔDCœύΫΜ”ΎΒψEΓΔFΘ§«“ΓœEAPΘΫ60ΓψΘ°
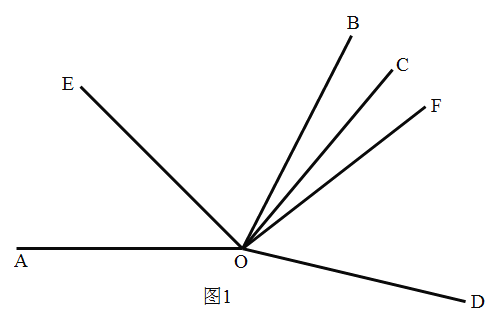
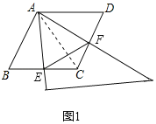
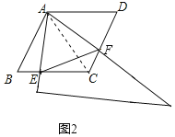
Θ®1Θ©»γΆΦ1Θ§Β±ΒψE «œΏΕΈCBΒΡ÷–Βψ ±Θ§«κ÷±Ϋ”≈–ΕœΓςAEFΒΡ–ΈΉ¥ «ΓΓ ΓΓΘ°
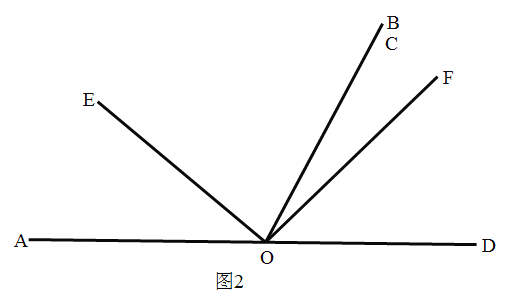
Θ®2Θ©»γΆΦ2Θ§Β±ΒψE «œΏΕΈCB…œ»Έ“β“ΜΒψ ±Θ®ΒψE≤Μ”κBΓΔC÷ΊΚœΘ©Θ§«σ÷ΛΘΚBEΘΫCFΘΜ
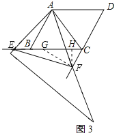
Θ®3Θ©»γΆΦ3Θ§Β±ΒψE‘ΎœΏΕΈCBΒΡ―”≥ΛœΏ…œΘ§«“ΓœEABΘΫ15Γψ ±Θ§«σΒψFΒΫBCΒΡΨύάκΘ°
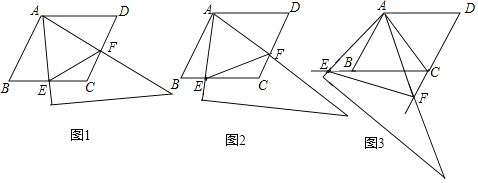
ΓΨ¥πΑΗΓΩΘ®1Θ©ΓςAEF «Β»±Ώ»ΐΫ«–ΈΘ§άμ”…ΦϊΫβΈωΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©ΒψFΒΫBCΒΡΨύάκΈΣ3©¹![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Ν§Ϋ”ACΘ§÷ΛΟςΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§ΒΟ≥ωACΘΫABΘ§‘Ό÷ΛΟςΓςBAEΓ’ΓςDAFΘ§ΒΟ≥ωAEΘΫAFΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©Ν§Ϋ”ACΘ§Ά§Θ®1Θ©ΒΟΘΚΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§ΒΟ≥ωΓœBACΘΫΓœACBΘΫ60ΓψΘ§ABΘΫACΘ§‘Ό÷ΛΟςΓςBAEΓ’ΓςCAFΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®3Θ©Ά§Θ®1Θ©ΒΟΘΚΓςABCΚΆΓςACD «Β»±Ώ»ΐΫ«–ΈΘ§ΒΟ≥ωABΘΫACΘ§ΓœBACΘΫΓœACBΘΫΓœACDΘΫ60ΓψΘ§÷ΛΟςΓςBAEΓ’ΓςCAFΘ§ΒΟ≥ωBEΘΫCFΘ§AEΘΫAFΘ§÷Λ≥ωΓςAEF «Β»±Ώ»ΐΫ«–ΈΘ§ΒΟ≥ωΓœAEFΘΫ60ΓψΘ§÷Λ≥ωΓœAEBΘΫ45ΓψΘ§ΒΟ≥ωΓœCEFΘΫΓœAEF©¹ΓœAEBΘΫ15ΓψΘ§ΉςFHΓΆBC”ΎHΘ§‘ΎΓςCEFΡΎ≤ΩΉςΓœEFGΘΫΓœCEFΘΫ15ΓψΘ§‘ρGEΘΫGFΘ§ΓœFGHΘΫ30ΓψΘ§”…÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωFGΘΫ2FHΘ§GHΘΫ![]() FHΘ§CFΘΫ2CHΘ§FHΘΫ
FHΘ§CFΘΫ2CHΘ§FHΘΫ![]() CHΘ§…ηCHΘΫxΘ§‘ρBEΘΫCFΘΫ2xΘ§FHΘΫ
CHΘ§…ηCHΘΫxΘ§‘ρBEΘΫCFΘΫ2xΘ§FHΘΫ![]() xΘ§GEΘΫGFΘΫ2FHΘΫ2
xΘ§GEΘΫGFΘΫ2FHΘΫ2![]() xΘ§GHΘΫ
xΘ§GHΘΫ![]() FHΘΫ3xΘ§ΒΟ≥ωEHΘΫ4+xΘΫ2
FHΘΫ3xΘ§ΒΟ≥ωEHΘΫ4+xΘΫ2![]() x+3xΘ§ΫβΒΟΘΚxΘΫ
x+3xΘ§ΫβΒΟΘΚxΘΫ![]() ©¹1Θ§«σ≥ωFHΘΫ
©¹1Θ§«σ≥ωFHΘΫ![]() xΘΫ3©¹
xΘΫ3©¹![]() Φ¥Ω…Θ°
Φ¥Ω…Θ°
Θ®1Θ©ΫβΘΚΓςAEF «Β»±Ώ»ΐΫ«–ΈΘ§άμ”…»γœ¬ΘΚ
Ν§Ϋ”ACΘ§»γΆΦ1Υυ ΨΘΚ
ΓΏΥΡ±Ώ–ΈABCD «Νβ–ΈΘ§
ΓύABΘΫBCΘΫADΘ§ΓœBΘΫΓœDΘ§
ΓΏΓœABCΘΫ60ΓψΘ§
ΓύΓœBADΘΫ120ΓψΘ§ΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύACΘΫABΘ§
ΓΏΒψE «œΏΕΈCBΒΡ÷–ΒψΘ§
ΓύAEΓΆBCΘ§
ΓύΓœBAEΘΫ30ΓψΘ§
ΓΏΓœEAFΘΫ60ΓψΘ§
ΓύΓœDAFΘΫ120Γψ©¹30Γψ©¹60ΓψΘΫ30ΓψΘΫΓœBAEΘ§
‘ΎΓςBAEΚΆΓςDAF÷–Θ§
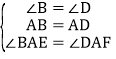 Θ§
Θ§
ΓύΓςBAEΓ’ΓςDAFΘ®ASAΘ©Θ§
ΓύAEΘΫAFΘ§
”÷ΓΏΓœEAFΘΫ60ΓψΘ§
ΓύΓςAEF «Β»±Ώ»ΐΫ«–ΈΘΜ
Ι ¥πΑΗΈΣΘΚΒ»±Ώ»ΐΫ«–ΈΘΜ
Θ®2Θ©÷ΛΟςΘΚΝ§Ϋ”ACΘ§»γΆΦ2Υυ ΨΘΚ
Ά§Θ®1Θ©ΒΟΘΚΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœBACΘΫΓœACBΘΫ60ΓψΘ§ABΘΫACΘ§
ΓΏΓœEAFΘΫ60ΓψΘ§
ΓύΓœBAEΘΫΓœCAFΘ§
ΓΏΓœBCDΘΫΓœBADΘΫ120ΓψΘ§
ΓύΓœACFΘΫ60ΓψΘΫΓœBΘ§
‘ΎΓςBAEΚΆΓςCAF÷–Θ§
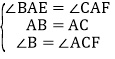 Θ§
Θ§
ΓύΓςBAEΓ’ΓςCAFΘ®ASAΘ©Θ§
ΓύBEΘΫCFΘΜ
Θ®3Θ©ΫβΘΚΆ§Θ®1Θ©ΒΟΘΚΓςABCΚΆΓςACD «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύABΘΫACΘ§ΓœBACΘΫΓœACBΘΫΓœACDΘΫ60ΓψΘ§
ΓύΓœACFΘΫ120ΓψΘ§
ΓΏΓœABCΘΫ60ΓψΘ§
ΓύΓœABEΘΫ120ΓψΘΫΓœACFΘ§
ΓΏΓœEAFΘΫ60ΓψΘ§
ΓύΓœBAEΘΫΓœCAFΘ§
‘ΎΓςBAEΚΆΓςCAF÷–Θ§
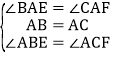 Θ§
Θ§
ΓύΓςBAEΓ’ΓςCAFΘ®ASAΘ©Θ§
ΓύBEΘΫCFΘ§AEΘΫAFΘ§
ΓΏΓœEAFΘΫ60ΓψΘ§
ΓύΓςAEF «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœAEFΘΫ60ΓψΘ§
ΓΏΓœEABΘΫ15ΓψΘ§ΓœABCΘΫΓœAEB+ΓœEABΘΫ60ΓψΘ§
ΓύΓœAEBΘΫ45ΓψΘ§
ΓύΓœCEFΘΫΓœAEF©¹ΓœAEBΘΫ15ΓψΘ§
ΉςFHΓΆBC”ΎHΘ§‘ΎΓςCEFΡΎ≤ΩΉςΓœEFGΘΫΓœCEFΘΫ15ΓψΘ§»γΆΦ3Υυ ΨΘΚ
‘ρGEΘΫGFΘ§ΓœFGHΘΫ30ΓψΘ§
ΓύFGΘΫ2FHΘ§GHΘΫ![]() FHΘ§
FHȧ
ΓΏΓœFCHΘΫΓœACF©¹ΓœACBΘΫ60ΓψΘ§
ΓύΓœCFHΘΫ30ΓψΘ§
ΓύCFΘΫ2CHΘ§FHΘΫ![]() CHΘ§
CHȧ
…ηCHΘΫxΘ§‘ρBEΘΫCFΘΫ2xΘ§FHΘΫ![]() xΘ§GEΘΫGFΘΫ2FHΘΫ2
xΘ§GEΘΫGFΘΫ2FHΘΫ2![]() xΘ§GHΘΫ
xΘ§GHΘΫ![]() FHΘΫ3xΘ§
FHΘΫ3xΘ§
ΓΏBCΘΫABΘΫ4Θ§
ΓύCEΘΫBC+BEΘΫ4+2xΘ§
ΓύEHΘΫ4+xΘΫ2![]() x+3xΘ§
x+3xȧ
ΫβΒΟΘΚxΘΫ![]() ©¹1Θ§
©¹1Θ§
ΓύFHΘΫ![]() xΘΫ3©¹
xΘΫ3©¹![]() Θ§
Θ§
Φ¥ΒψFΒΫBCΒΡΨύάκΈΣ3©¹![]() Θ°
Θ°

 –¬ΩΈ±ξΩλά÷Χα”≈ νΦΌΉς“Β…¬Ές¬Ο”Έ≥ωΑφ…γœΒΝ–¥πΑΗ
–¬ΩΈ±ξΩλά÷Χα”≈ νΦΌΉς“Β…¬Ές¬Ο”Έ≥ωΑφ…γœΒΝ–¥πΑΗ νΦΌœΈΫ”≈ύ”≈ΫΧ≤Ρ’ψΫ≠ΙΛ…Χ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌœΈΫ”≈ύ”≈ΫΧ≤Ρ’ψΫ≠ΙΛ…Χ¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ –ά”οΈΡΜ·Ωλά÷ νΦΌ…ρ―τ≥ωΑφ…γœΒΝ–¥πΑΗ
–ά”οΈΡΜ·Ωλά÷ νΦΌ…ρ―τ≥ωΑφ…γœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ‘ΎΓΑ‘Σ©ñԾΦδΘ§ΤΫΦέ…Χ≥ΓΕ‘ΗΟ…Χ≥Γ…ΧΤΖΫχ––»γœ¬ΒΡ”≈Μί¥ΌœζΜνΕ·ΘΚ
¥ρ’έ«Α“Μ¥Έ–‘ΙΚΈοΉήΫπΕν | ”≈Μί¥κ © |
–Γ”ΎΒ»”Ύ 400 ‘Σ | ≤Μ”≈Μί |
≥§Ιΐ 400 ‘ΣΘ§ΒΪ≤Μ≥§Ιΐ 600‘Σ | Α¥ έΦέ¥ρΨ≈’έ |
≥§Ιΐ 600 ‘Σ | Τδ÷– 600 ‘Σ≤ΩΖ÷ΑΥ’έ”≈ΜίΘ§≥§Ιΐ 600 ‘ΣΒΡ≤ΩΖ÷¥ρΝυ’έ”≈Μί |
Α¥…œ ω”≈ΜίΧθΦΰΘ§»τ–ΓΜΣ“Μ¥Έ–‘ΙΚ¬ρ έΦέΈΣ 80 ‘Σ/ΦΰΒΡ…ΧΤΖ n Φΰ ±Θ§ ΒΦ ΗΕΩν 504 ‘ΣΘ§ ‘ρ n=_____.