题目内容
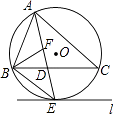
【题目】如图，已知∠AOB，OA=OB，点E在OB 上，四边形AEBF是矩形． 
（1）请你只用无刻度的直尺在图中画出∠AOB的平分线（保留画图痕迹）；
（2）若∠AOB=45°，OA=OB=2 
，求BE的长．
【答案】
（1）解：如图所示，OP即为所求；
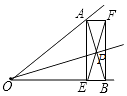
（2）解：在矩形AEBF中，AE⊥OB，∠AOB=45°，
∴OE=cos45°×2 
=2，
∴EB=2 ﹣2
【解析】（1）根据矩形的对角线相等且互相平分，运用三线合一即可画出∠AOB的平分线；（2）根据矩形AEBF中，AE⊥OB，∠AOB=45°，可得OE=cos45°×2 =2，即可得出EB=2 ﹣2．
【考点精析】关于本题考查的等腰三角形的性质和矩形的性质，需要了解等腰三角形的两个底角相等（简称：等边对等角）；矩形的四个角都是直角，矩形的对角线相等才能得出正确答案．
A加金题 系列答案
全优测试卷系列答案
【题目】某中学九年级1班同学积极响应“阳光体育工程”的号召，利用课外活动时间积极参加体育锻炼，每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练，训练前后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表．
进球数（个） | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
训练后篮球定时定点投篮测试进球数统计表
请你根据图表中的信息回答下列问题：
（1）选择长跑训练的人数占全班人数的百分比为 ， 该班学生的总人数为；
（2）训练后篮球定时定点投篮人均进球数为；
（3）若将选择篮球的同学的进球数写在外观、大小一样的枝条上，放在不透明的盒子中，搅拌均匀后，从中抽取一张，则抽到4的概率是多少？
【题目】阅读下列材料：
社会消费品零售总额是指批发和零售业，住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额，在各类与消费有关的统计数据中，社会消费品零售总额是表现国内消费需求最直接的数据．
2012年，北京市全年实现社会消费品零售总额7702.8亿元，比上一年增长11.6%，2013年，全年实现社会消费品零售总额8375.1亿元，比上一年增长8.7%，2014年，全年实现社会消费品零售总额9098.1亿元，比上一年增长8.6%，2015年，全年实现社会消费品零售总额10338亿元，比上一年增长7.3%．
2016年，北京市实现市场总消费19926.2亿元，比上一年增长了8.1%，其中实现服务性消费8921.1亿元，增长10.1%；实现社会消费品零售总额11005.1亿元，比上一年增长了6.5%．
根据以上材料解答下列问题：
（1）补全统计表：
2012﹣2016年北京市社会消费品零售总额统计表
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
社会消费品零售总额（单位：亿元） |
（2）选择适当的统计图将2012﹣2016年北京市社会消费品零售总额比上一年的增长率表示出来，并在图中表明相应数据；
（3）根据以上信息，估计2017年北京市社会消费品零售总额比上一年的增长率约为 ， 你的预估理由是 ．