Question

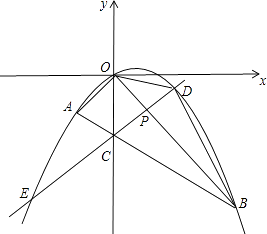
【题目】如图，经过坐标原点的抛物线C1：y=ax2+bx与x轴的另一交点为M，它的顶点为点A，将C1绕原点旋转180°，得到抛物线C2 ， C2与x轴的另一交点为N，顶点为点B，连接AM，MB，BN，NA，当四边形AMBN恰好是矩形时，则b的值（ ）

A.2
B.﹣2
C.2
D.﹣2

Answer 1

【答案】C
【解析】连接OA，作AD⊥OM，

∵四边形AMBN是矩形，∴OA=OM，

∵抛物线顶点为A，于x轴交于O，M点，

∴OA=AM，∴△OAM为等边三角形，∴AD= OM，

∵当y=0时，ax2+bx=0，解得：x=0或﹣ ，

∵抛物线C1：y=ax2+bx对称轴为﹣ ，将x=﹣ 代入得：y=a +b（ ），∴AD=a +b（ ）

∴a +b（ ）=AD= OM= （﹣ ），化简得：b= ，

所以答案是：C．

【考点精析】认真审题，首先需要了解二次函数图象的平移(平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减)，还要掌握抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．)的相关知识才是答题的关键．