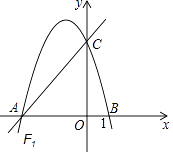题目内容
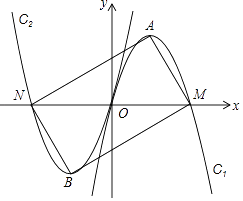
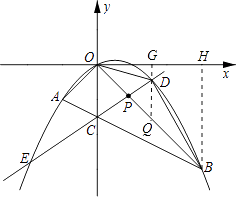
【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
【答案】
(1)解:解方程x2﹣2x﹣3=0,
得 x1=3,x2=﹣1.
∵m<n,
∴m=﹣1,n=3
∴A(﹣1,﹣1),B(3,﹣3).
设直线AB的解析式为y=kx+b
∴ ![]() ,
,
解得: 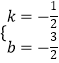 ,
,
所以直线AB的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ;
;
设直线OB的解析式为y=kx,
∴3k=﹣3,
解得:k=﹣1,
∴直线OB的解析式为y=﹣x
(2)解:∵抛物线过原点,设抛物线的解析式为y=ax2+bx(a≠0).
∴ ![]() ,
,
解得: 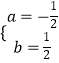 ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x
x
(3)解:△BOD的面积是存在最大值;
过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
设Q(x,﹣x),D(x,﹣ ![]() x2+
x2+ ![]() x).
x).
S△BOD=S△ODQ+S△BDQ= ![]() DQOG+
DQOG+ ![]() DQGH,
DQGH,
= ![]() DQ(OG+GH),
DQ(OG+GH),
= ![]() [x+(﹣
[x+(﹣ ![]() x2+
x2+ ![]() x)]×3,
x)]×3,
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∵0<x<3,
∴当x= ![]() 时,S取得最大值为
时,S取得最大值为 ![]() ,此时D(
,此时D( ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)首先解方程得出A,B两点的坐标,利用待定系数法确定直线AB和直线OB的解析式即可;(2)利用待定系数法求出二次函数解析式即可;(3)利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数,进而得出最值即可.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案