题目内容
(1)计算:-12× +|-3
+|-3 |+2cos60°;
|+2cos60°;
(2)解方程: -
-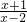 =1;
=1;
(3)解不等式组: ,并写出它的所有整数解.
,并写出它的所有整数解.
解:(1)原式=-1×3 +3
+3 +2×
+2× ,
,
=-3 +3
+3 +1,
+1,
=1,
(2)去分母得:2x(x-2)-(x-3)(x+1)=(x-3)(x-2),
去括号得:2x2-2x-x2+2x+3=x2-5x+6.
移项得:2x2-2x+2x-x2-x2+5x=6-3,
合并同类项得:5x=3,
把x的系数化为1:x= ,
,
检验:把x= 代入最简公分母(x-3)(x-2)≠0,
代入最简公分母(x-3)(x-2)≠0,
∴原分式方程的解为:x= ,
,
(3)由①得:x≤3,
由②得:x>1,
∴不等式组的解集为:3≥x>1,
∴整数解为:2,3.
分析:(1)此题涉及到了二次根式的化简,乘方,绝对值,特殊角的三角函数值,首先根据各知识点计算,然后再算乘法,最后计算加减法即可.
(2)首先乘以最简公分母去分母,然后去括号,移项,合并同类项,把x的系数化为1,最后一定要检验.
(3)分别解出两个不等式的解集,然后再取公共解集再写出整数解即可.
点评:此题主要考查了不等式组的解法,分式方程的解法,以及二次根式的化简,乘方,绝对值,特殊角的三角函数值,实数运算,解题的关键是准确把握各个知识点.
 +3
+3 +2×
+2× ,
,=-3
 +3
+3 +1,
+1,=1,
(2)去分母得:2x(x-2)-(x-3)(x+1)=(x-3)(x-2),
去括号得:2x2-2x-x2+2x+3=x2-5x+6.
移项得:2x2-2x+2x-x2-x2+5x=6-3,
合并同类项得:5x=3,
把x的系数化为1:x=
 ,
,检验:把x=
 代入最简公分母(x-3)(x-2)≠0,
代入最简公分母(x-3)(x-2)≠0,∴原分式方程的解为:x=
 ,
,(3)由①得:x≤3,
由②得:x>1,
∴不等式组的解集为:3≥x>1,
∴整数解为:2,3.
分析:(1)此题涉及到了二次根式的化简,乘方,绝对值,特殊角的三角函数值,首先根据各知识点计算,然后再算乘法,最后计算加减法即可.
(2)首先乘以最简公分母去分母,然后去括号,移项,合并同类项,把x的系数化为1,最后一定要检验.
(3)分别解出两个不等式的解集,然后再取公共解集再写出整数解即可.
点评:此题主要考查了不等式组的解法,分式方程的解法,以及二次根式的化简,乘方,绝对值,特殊角的三角函数值,实数运算,解题的关键是准确把握各个知识点.

练习册系列答案
相关题目
 如图所示,把一个面积为1的正方形等分成两个面积为
如图所示,把一个面积为1的正方形等分成两个面积为