题目内容
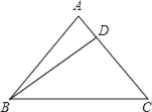
【题目】如图,客轮沿折线A—B—C从A点出发经过B点再到C点匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批货物送达客轮,两船同时起航,并同时到达折线A—B—C上的某点E处,已知AB=BC=200海里,∠ABC=90°,客轮的速度是货轮速度的2倍.
(1)选择题:两船相遇之处E点( )
A.在线段AB上
B.在线段BC上
C.可能在线段AB上,也可能在线段BC上
(2)货轮从出发到两船相遇共航行了多少海里?

【答案】(1)B;(2) (200-![]() )海里.
)海里.
【解析】
由于△ABC是等腰直角三角形,D为AC的中点,而客轮速度是货轮速度的2倍,从出发到相遇,客轮走的路程应是货轮的2倍,根据等腰直角三角形性质和三角形三边关系,不难判断两轮相遇的大致位置;
(2)设货轮从出发到两船相遇共航行了x海里,过D点作DF⊥CB于F,连接DE,则DE=x,AB+BE=2x,根据D点是AC的中点,得DF=![]() AB=100,EF=400-100-2x,在Rt△DFE中,DE2=DF2+EF2,得x2=1002+(300-2x)2解方程求解即可.
AB=100,EF=400-100-2x,在Rt△DFE中,DE2=DF2+EF2,得x2=1002+(300-2x)2解方程求解即可.
解:(1) (1)若货轮沿DB方向航行,∵△ABC为等腰直角三角形,点D为AC中点,
∴AD=BD.
由三角形三边关系,知AD+BD>AB,
即2BD>AB,
因此两轮不可能在AB边上相遇,
所以两轮只能在BC边上相遇.
故选B.
(2)设货轮从出发到两船相遇共航行了x海里,过D点作DF⊥CB于F,连结DE,DB,如图,则DE=x海里,AB+BE=2x海里,
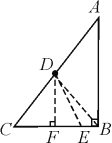
∵D点是AC的中点,
∴DF=![]() AB=100海里,EF=(400-100-2x)海里,
AB=100海里,EF=(400-100-2x)海里,
在Rt△DFE中,DE2=DF2+EF2,得x2=1002+(300-2x)2,
解得x=200±![]() ,
,
∵200+![]() >
>![]() 不合题意,舍去,
不合题意,舍去,
∴DE=(200-![]() )海里.
)海里.
答:货轮从出发到两船相遇共航行了(200-![]() )海里.
)海里.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案