题目内容
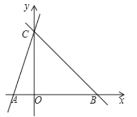
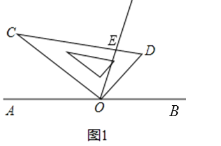
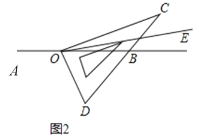
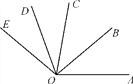
【题目】如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
【答案】40°.
【解析】试题分析:(1)根据角平分线的定义可以求得∠BOD=∠AOB+∠DOE;
(2)根据角平分线的定义易求得∠EOC=2∠COD=60°,所以由图中的角与角间的和差关系可以求得∠AOC=80°,最后由角平分线的定义求解.
试题解析:解:(1)因为OB为∠AOC的平分线,OD是∠COE的平分线,
所以∠AOB=∠BOC,∠DOE=∠DOC.
所以∠BOD=∠BOC+∠DOC=∠AOB+∠DOE=40°+30°=70°.
(2)因为OD是∠COE的平分线,∠COD=30°,
所以∠EOC=2∠COD=60°.
因为∠AOE=140°,∠AOC=∠AOE-∠EOC=80°.
又因为OB为∠AOC的平分线,
所以∠AOB=![]() ∠AOC=40°.
∠AOC=40°.

练习册系列答案
相关题目
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示.
时间段(小时/周) | 小丽抽样(人数) | 小杰抽样(人数) |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(1)你认为哪位学生抽取的样本不合理?请说明理由.
(2)专家建议每周上网2小时以上(含2小时)的学生应适当减少上网的时间,估计该校全体初二学生中有多少名学生应适当减少上网的时间.