题目内容
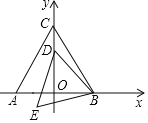
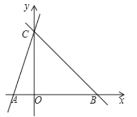
【题目】如图,直线y=kx+k交x轴,y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45.
(1)求直线BC的解析式;
(2)动点P从A出发沿射线AB匀速运动,速度为2个单位/秒,连接CP,设△PBC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,直接写出t的取值范围;
【答案】(1) BC的解析式是y=x+3;(2)当0<t2时, S=3t+6;当t>2时,S=3t6.
【解析】
(1)令y=0,即可求得A的坐标,根据OC=3OA即可求得C的坐标,再根据∠CBA=45°,即△BOC的等腰直角三角形,则B的坐标即可求得,然后利用待定系数法求得BC的解析式;
(2)分成P在AB和在AB的延长线上两种情况进行讨论,利用三角形面积公式即可求解.
(1)在y=kx+k中,令y=0,则x=1,即A的坐标是(1,0).
∵OC=3OA,
∴OC=3,即C的坐标是(0,3).
∵∠CBA=45,
∴∠OCB=∠CBA=45,
∴OB=OC=3,则B的坐标是(3,0).
设BC的解析式是y=kx+b,则![]() ,
,
解得:![]() ,
,
则BC的解析式是y=x+3;
(2)当0<t2时,P在线段AB上,则BP=42t,
则S=![]() (42t)×3=3t+6;
(42t)×3=3t+6;
当t>2时,OP=2t4,则S=![]() ×3(2t4),即S=3t6.
×3(2t4),即S=3t6.

练习册系列答案
相关题目