题目内容
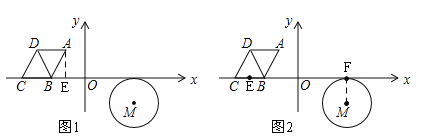
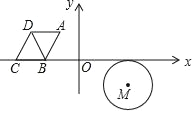
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,﹣1),点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与BC相切,且切点为BC的中点时,连接BD,求:
①t的值;
②∠MBD的度数;
(3)在(2)的条件下,当点M与BD所在的直线的距离为1时,求t的值.
【答案】(1)8;(2)①7;②105°;(3)t=6﹣![]() 或6+
或6+![]() .
.
【解析】分析:(1)根据勾股定理求菱形的边长为2,所以可得周长为8;
(2)①如图2,先根据坐标求EF的长,由EE'﹣FE'=EF=7,列式得:3t﹣2t=7,可得t的值;
②先求∠EBA=60°,则∠FBA=120°,再得∠MBF=45°,相加可得:∠MBD=∠MBF+∠FBD=45°+60°=105°;
(3)分两种情况讨论:作出距离MN和ME,第一种情况:如图5由距离为1可知:BD为⊙M的切线,由BC是⊙M的切线,得∠MBE=30°,列式为3t+![]() =2t+6,解出即可;
=2t+6,解出即可;
第二种情况:如图6,同理可得t的值.
详解:(1)如图1,过A作AE⊥BC于E.
∵点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),∴AE=
),点B的坐标为(﹣3,0),∴AE=![]() ,BE=3﹣2=1,∴AB=
,BE=3﹣2=1,∴AB=![]() =
=![]() =2.
=2.
∵四边形ABCD是菱形,∴AB=BC=CD=AD=2,∴菱形ABCD的周长=2×4=8;
(2)①如图2,⊙M与x轴的切点为F,BC的中点为E.
∵M(3,﹣1),∴F(3,0).
∵BC=2,且E为BC的中点,∴E(﹣4,0),∴EF=7,即EE'﹣FE'=EF,∴3t﹣2t=7,t=7;
②由(1)可知:BE=1,AE=![]() ,
,
∴tan∠EBA=![]() =
=![]() =
=![]() ,∴∠EBA=60°,如图4,∴∠FBA=120°.
,∴∠EBA=60°,如图4,∴∠FBA=120°.
∵四边形ABCD是菱形,∴∠FBD=![]() ∠FBA=
∠FBA=![]() =60°.
=60°.
∵BC是⊙M的切线,∴MF⊥BC.
∵F是BC的中点,∴BF=MF=1,∴△BFM是等腰直角三角形,
∴∠MBF=45°,∴∠MBD=∠MBF+∠FBD=45°+60°=105°;
(3)连接BM,过M作MN⊥BD,垂足为N,作ME⊥BC于E,分两种情况:
第一种情况:如图5.
∵四边形ABCD是菱形,∠ABC=120°,∴∠CBD=60°,∴∠NBE=60°.
∵点M与BD所在的直线的距离为1,∴MN=1,∴BD为⊙M的切线.
∵BC是⊙M的切线,∴∠MBE=30°.
∵ME=1,∴EB=![]() ,∴3t+
,∴3t+![]() =2t+6,t=6﹣
=2t+6,t=6﹣![]() ;
;
第二种情况:如图6.
∵四边形ABCD是菱形,∠ABC=120°,∴∠DBC=60°,∴∠NBE=120°.
∵点M与BD所在的直线的距离为1,∴MN=1,∴BD为⊙M的切线.
∵BC是⊙M的切线,∴∠MBE=60°.
∵ME=MN=1,∴Rt△BEM中,tan60°=![]() ,EB=
,EB=![]() =
=![]() ,
,
∴3t=2t+6+![]() ,t=6+
,t=6+![]() ;
;
综上所述:当点M与BD所在的直线的距离为1时,t=6﹣![]() 或6+
或6+![]() .
.