题目内容
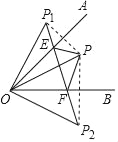
【题目】已知∠AOB=45°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,连接P1P2交OA、OB于E、F,若P1E=![]() ,OP=
,OP=![]() ,则EF的长度是_____.
,则EF的长度是_____.
【答案】![]()
【解析】
由P,P1关于直线OA对称,P、P2关于直线OB对称,推出OP=OP1=OP2,∠AOP=∠AOP1,∠BOP=∠BOP2,推出∠P1OP2=90°,由此即可判断△P1OP2是等腰直角三角形,由轴对称可得,∠OPE=∠OP1E=45°,∠OPF=∠OP2F=45°,进而得出∠EPF=90°,最后依据勾股定理列方程,即可得到EF的长度.
∵P,P1关于直线OA对称,P、P2关于直线OB对称,
∴OP=OP1=OP2=![]() ,∠AOP=∠AOP1,∠BOP=∠BOP2,
,∠AOP=∠AOP1,∠BOP=∠BOP2,
∵∠AOB=45°,
∴∠P1OP2=2∠AOP+2∠BOP=2(∠AOP+∠BOP)=90°,
∴△P1OP2是等腰直角三角形,
∴P1P2=![]() =2,
=2,
设EF=x,
∵P1E=![]() =PE,
=PE,
∴PF=P2F=![]() -x,
-x,
由轴对称可得,∠OPE=∠OP1E=45°,∠OPF=∠OP2F=45°,
∴∠EPF=90°,
∴PE2+PF2=EF2,即(![]() )2+(
)2+(![]() -x)2=x2,
-x)2=x2,
解得x=![]() .
.
故答案为:![]() .
.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目