Question

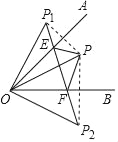
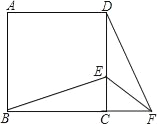
【题目】如图，正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE=CF．

（1）求证：△BCE≌△DCF；

（2）若∠BEC=60°，求∠EFD的度数．

Answer 1

【答案】（1）见解析；（2）∠EFD=15°．

【解析】

试题（1）可利用边角边证明BE、DF所在的两个直角三角形全等，进而证明这两条线段相等；
（2）由（1）中的全等可得∠DFC=∠BEC=60°，易得∠CFE=45°，相减即可得到所求角的度数．

试题解析：（1）证明：∵ABCD是正方形，

∴DC=BC，∠DCB=∠FCE，

∵CE=CF，

∴△DCF≌△BCE；

（2）∵△BCE≌△DCF，

∴∠DFC=∠BEC=60°，

∵CE=CF，

∴∠CFE=45°，

∴∠EFD=15°．