Question

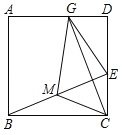
【题目】如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连接OD，∠AOD＝∠APC.

(1)求证：AP是⊙O的切线；

(2)若⊙O的半径是4，AP＝4，求图中阴影部分的面积．

Answer 1

【答案】(1)证明见解析;(2) =.

【解析】试题分析：（1）连接OP，要证AP是⊙O的切线，只需 根据条件证得∠APO=90°即可；（2）分别求出△DPO和扇形OPBD的面积，然后利用S阴影=S扇形OPBD－S△OPD计算即可．

试题解析：解：（1）证明：连接OP，则OD=OP，

∴∠OPD=∠ODP，

∴∠APC=∠AOD，

∴∠OPD+∠APC=∠ODP+∠AOD，

又∵PD⊥BE，

∴∠ODP+∠AOD=90°，

则∠OPD+∠APC=90°，

即∠APO=90°，

∴AP是⊙O的切线．

（2）解：在Rt△APO中，

∵AP=，PO=4，

∴AO=，即PO= ，

∴∠A=30°，

可知∠POA=60°，

又∵PD⊥BE，

∴∠OPC=30°且PC=CD，∠POD=120°，

∴OC=PO=2，

则,

∴PD=2PC=，

∴S阴影=S扇形OPBD－S△OPD

=

=