题目内容
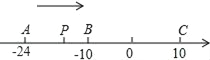
【题目】如图,数轴上 A、B 两点所对应的数分别是 a 和 b,且(a+5)2+|b﹣7|=0.
(1)求 a,b;A、B 两点之间的距离.
(2)有一动点 P 从点 A 出发第一次向左运动 1 个单位长度,然后在新的位置第二次运动,向右运动 2个单位长度,在此位置第三次运动,向左运动 3个单位长度…按照如此规律不断地左右运动,当运动到 2019次时,求点P所对应的数.
(3)在(2)的条件下,点 P在某次运动时恰好到达某一个位置,使点 P到点B的距离是点 P 到点 A 的距离的3倍?请直接写出此时点 P所对应的数,并分别写出是第几次运动.
![]()
【答案】(1)a=﹣5,b=7,12;(2)点 P 所对应的数为﹣1015;(3)﹣11 和﹣2 分别是点 P 运动了第 11 次和第 6 次到达的位置.
【解析】
(1)根据二次多项式的定义得到 a+5=0,由此求得 a 的值;然后由多项式的系数的定义得到 b 的值,则易求线段 AB 的值;
(2)根据题意得到点 P 每一次运动后所在的位置,然后由有理数的加法进行计算即可;
(3)设点 P 对应的有理数的值为 x,分情况进行解答:点 P 在点 A 的左侧,点 P在点 A、B 之间、点 P 在点 B 的右侧三种情况.
(1)∵(a+5)2+|b﹣7|=0,
∴a+5=0,b﹣7=0,
∴a=﹣5,b=7;
∴A、B两点之间的距离=|﹣5|+7=12;
(2)设向左运动记为负数,向右运动记为正数,
依题意得:﹣5﹣1+2﹣3+4﹣5+6﹣7+…+2018﹣2019=﹣5+1009﹣2019=﹣1015.
答:点P所对应的数为﹣1015;
(3)设点P对应的有理数的值为x,
①当点P在点A的左侧时:PA=﹣5﹣x,PB=7﹣x,
依题意得:7﹣x=3(﹣5﹣x),解得:x=﹣11;
②当点P在点A和点B之间时:PA=x﹣(﹣5)=x+5,PB=7﹣x,
依题意得:7﹣x=3(x+5),
解得:x=﹣2;
③当点P在点B的右侧时:PA=x﹣(﹣5)=x+5,PB=x﹣7,
依题意得:x﹣7=3(x+5),
解得:x=﹣11,这与点P在点B的右侧(即 x>7)矛盾,故舍去.
综上所述,点P所对应的有理数分别是﹣11和﹣2.
所以﹣11和﹣2分别是点P运动了第11次和第6次到达的位置.