Question

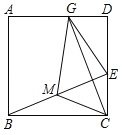
【题目】如图，在正方形ABCD中，E是边CD上一点(点E不与点C、D重合)，连结BE，取BE的中点M，连结CM．过点C作CG⊥BE交AD于点G，连结EG、MG．若CM=3，则四边形GMCE的面积为____．

Answer 1

【答案】9．

【解析】

证明△BCE≌△CDG（ASA），可得BE=CG，根据直角三角形斜边中线的性质可得CG=BE=2CM=6，最后根据面积和可得四边形GMCE的面积．

解：令BE、CG交于点O，

∵四边形ABCD是正方形，

∴BC=CD，∠D=∠BCE=90°．

∵CG⊥BE，

∴∠COE=∠CEO+∠ECO=∠CEO+∠CBE=90°，

∴∠ECO=∠CBE，

在△BCE和△CDG中，

∵ ，

∴△BCE≌△CDG(ASA)，

∴BE=CG．

∵CM=3，∠BCE=90°，且M是BE的中点，

∴CG=BE=2CM=6，

∴四边形GMCE的面积=S△EMG+S△CME=．

故答案为：9．