题目内容
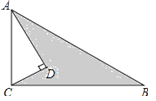
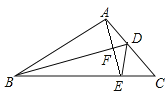
【题目】如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE.
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长;
(2)若![]() ,
,![]() ,求
,求![]() 度数.
度数.
【答案】(1)6;(2)57°
【解析】
(1)根据线段垂直平分线的性质得到AB=BE,DA=DE,然后利用三角形的周长求AB得长度;(2)利用三角形外角的性质求∠ADB的度数,然后利用等腰三角形三线合一的性质求∠ADE的度数,从而使问题得解.
解:(1)∵BD垂直平分AE,垂足为F,交AC于点D
∴AB=BE,DA=DE
∴△DEC的周长=DE+DC+EC=DA+DC+EC=AC+EC=6
△ABC的周长=AB+BC+AC=AB+BE+EC+AC=AB+AB+AC+EC=18
∴2AB=18-6=12
∴AB=6
(2)由(1)可知,BD垂直平分AE ,AB=BE,DA=DE
∴根据等腰三角形三线合一的性质可知∠DBC=![]() ∠ABC=
∠ABC=![]() =14.5°
=14.5°
∠ADB=∠BDE=∠DBC+∠C=14.5°+47°=61.5°
∴∠CDE=180°-61.5°×2=57°

练习册系列答案
相关题目