题目内容
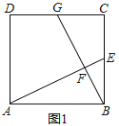
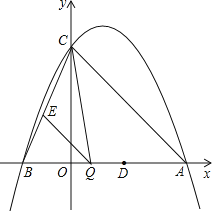
【题目】已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该二次函数的关系式;
(2)写出该二次函数的对称轴和顶点坐标;
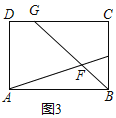
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
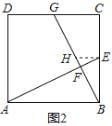
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2+x+4;(2)二次函数的对称轴为:直线x=1,顶点坐标为:(1,
x2+x+4;(2)二次函数的对称轴为:直线x=1,顶点坐标为:(1,![]() );(3)Q点坐标为(1,0);(4)存在,点P的坐标为:P(1+
);(3)Q点坐标为(1,0);(4)存在,点P的坐标为:P(1+![]() ,2)或P(1-
,2)或P(1-![]() ,2)或P(1+
,2)或P(1+![]() ,3)或P(1-
,3)或P(1-![]() ,3).
,3).
【解析】
(1)根据A,C两点坐标,利用待定系数法求二次函数解析式即可;
(2)根据配方法求出二次函数的顶点坐标和对称轴即可;
(3)利用相似三角形的性质得出S△CQE=![]() x×4-
x×4-![]() x2=-
x2=-![]() x2+2x,进而求出即可;
x2+2x,进而求出即可;
(4)利用图象以及等腰三角形的性质假设若DO=DF时以及当FO=FD和当OF=OD时分别得出F点的坐标,将纵坐标代入二次函数解析式即可求出P点坐标.
(1)∵点C(0,4),
∴c=4,
∵点A的坐标为(4,0),
∴0=16a-8a+4,
∴a=-![]() ,
,
∴y=-![]() x2+x+4;
x2+x+4;
(2)y=-![]() x2+x+4
x2+x+4
=-![]() (x2-2x)+4,
(x2-2x)+4,
=-![]() [(x2-2x+1)-1]+4,
[(x2-2x+1)-1]+4,
=-![]() (x-1)2+
(x-1)2+![]() ,
,
∴该二次函数的对称轴为:直线x=1,顶点坐标为:(1,![]() );
);
(3)∵二次函数的对称轴为:直线x=1,点A的坐标为(4,0),
∴B(-2,0,),AB=6,
S△ABC=![]() ×6×4=12,
×6×4=12,
设BQ=x,
∵EQ∥AC,
∴△BEQ∽△BCA,
∴(![]() )2=
)2=![]() ,
,
∴S△BEQ=![]() ,
,
∴S△CQE=![]() x×4-
x×4-![]() =-
=-![]() +2x,
+2x,
当x=-![]() =3时,△CQE面积最大,
=3时,△CQE面积最大,
∴Q点坐标为(1,0);
(4)存在,
在△ODF中,
①若DO=DF,∵A(4,0),D(2,0),
∴AD=OD=DF=2,
又∵在Rt△AOC中,OA=OC=4,
∴∠OAC=45°,
∴∠DFA=∠OAC=45°,
∴∠ADF=90°,此时,点F的坐标为:(2,2),
由-![]() x2+x+4=2,
x2+x+4=2,
解得:x1=1+![]() ,x2=1-
,x2=1-![]() ,
,
此时,点P的坐标为:P(1+![]() ,2)或P(1-
,2)或P(1-![]() ,2);
,2);
②若FO=FD,过点F作FM⊥x轴于点M,

由等腰三角形的性质得出:
OM=![]() OD=1,
OD=1,
∴AM=3,
∴在等腰三角形△AMF中,MF=MA=3,
∴F(1,3),
由-![]() x2+x+4=3,
x2+x+4=3,
解得:x1=1+![]() ,x2=1-
,x2=1-![]() ,
,
此时,点P的坐标为:P(1+![]() ,3)或P(1-
,3)或P(1-![]() ,3);
,3);
③若OD=OF,∵OA=OC=4,且∠AOC=90°,
∴AC=4![]() ,
,
∴点O到AC的距离为2![]() ,而OF=OD=2<2
,而OF=OD=2<2![]() ,
,
∴此时,不存在这样的直线l,使得△ODF是等腰三角形.
综上所述:存在这样的直线l,使得△ODF是等腰三角形,所求点P的坐标为:P(1+![]() ,2)或P(1-
,2)或P(1-![]() ,2)或P(1+
,2)或P(1+![]() ,3)或P(1-
,3)或P(1-![]() ,3).
,3).

【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表,请根据图表中提供的信息解答下列问题:
AQI指数 | 质量等级 | 天数(天) |
0-50 | 优 | m |
51-100 | 良 | 44 |
101-150 | 轻度污染 | n |
151-200 | 中度污染 | 4 |
201-300 | 重度污染 | 2 |
300以上 | 严重污染 | 2 |

(1)统计表中m= ,n= ,扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少?
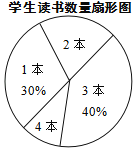
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?