Question

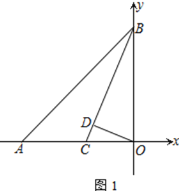
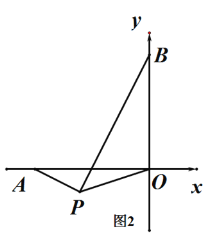
【题目】如图，数轴上，两点对应的有理数分别为和12，点从点出发，以每秒1个单位长度的速度沿数轴负方向运动，点同时从点出发，以每秒2个单位长度的速度沿数轴正方向运动，设运动时间为秒．

（1）求经过2秒后,数轴点、分别表示的数；

（2）当时，求的值；

（3）在运动过程中是否存在时间使，若存在，请求出此时的值，若不存在，请说明理由．

Answer 1

【答案】（1）表示，表示4；（2）；（3）存在，或．

【解析】

（1）根据点P，Q的运动速度及方向可找出t秒时点P，Q表示的数，再代入t=2即可得出结论；
（2）代入t=3可找出点P，Q表示的数，再利用两点间的距离公式可求出PQ的值；
（3）由点A，B表示的数了找出AP，BQ的值，结合AP=BQ可得出关于t的一元一次方程，解之即可得出结论．

解：（1）∵点P从点O出发，以每秒1个单位长度的速度沿数轴负方向运动，点Q同时从点O出发，以每秒2个单位长度的速度沿数轴正方向运动，
∴运动时间为t秒时，点P表示的数为-t，点Q表示的数为2t，
∴当t=2时，点P表示的数为-2，点Q表示的数为4．
（2）当t=3时，点P表示的数为-3，点Q表示的数为6，
∴PQ=6-（-3）=9．
（3）∵点A表示的数为-8，点B表示的数为12，
∴AP=|-t-（-8）|=|8-t|，BQ=|2t-12|．
∵AP=BQ，
∴|8-t|=|2t-12|，
即8-t=2t-12或t-8=2t-12，
解得：或t=4，
∴当AP=BQ时，t的值为秒或4秒．