题目内容
(2012•乐山模拟)在锐角△ABC中,AB=AC,∠A使关于x的方程
x2-sinA•x+
sinA-
=0有两个相等的实数根.
(1)判断△ABC的形状;
(2)设D为BC上的一点,且DE⊥AB于E,DF⊥AC于F,若DE=m,DF=n,且3m=4n和m2+n2=25,求AB的长.
| 1 |
| 4 |
| 3 |
| 3 |
| 4 |
(1)判断△ABC的形状;
(2)设D为BC上的一点,且DE⊥AB于E,DF⊥AC于F,若DE=m,DF=n,且3m=4n和m2+n2=25,求AB的长.
分析:(1)利用根的判别式求出sinA=
,进而得出∠A=60°,再利用AB=AC,求出△ABC的形状.
(2)根据题意可得出∠BDE=∠CDF=30°,再由锐角三角函数关系可得出BD,CD,从而求出BC进而得出AB的长.
| ||
| 2 |
(2)根据题意可得出∠BDE=∠CDF=30°,再由锐角三角函数关系可得出BD,CD,从而求出BC进而得出AB的长.
解答:解:(1)∵关于x的方程
x2-sinA•x+
sinA-
=0有两个相等的实数根,
∴b2-4ac=sin2A-4×
(
sinA-
)=0,
则(sinA-
)2=0,
故sinA-
=0,
即sinA=
,
解得:∠A=60°,
又∵AB=AC,
∴△ABC的形状为等边三角形;
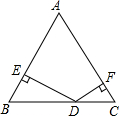
(2)解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵DE⊥AB于E,DF⊥AC于F,
∴∠BED=∠CFD=90°,∴∠EDB=∠FDC=30°,
∵DE=m,DF=n,且3m=4n和m2+n2=25,
∴m=
,
∴(
)2+n2=25,
解得:n=3,则m=4,
∴DE=4,DF=3,
∵cos30°=
,
∴BD=
=
=
,
∵cos30°=
,
∴CD=
=2
,
∴BC=
+2
=
,
则AB的长为
.
| 1 |
| 4 |
| 3 |
| 3 |
| 4 |
∴b2-4ac=sin2A-4×
| 1 |
| 4 |
| 3 |
| 3 |
| 4 |
则(sinA-
| ||
| 2 |
故sinA-
| ||
| 2 |
即sinA=
| ||
| 2 |
解得:∠A=60°,
又∵AB=AC,
∴△ABC的形状为等边三角形;

(2)解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵DE⊥AB于E,DF⊥AC于F,
∴∠BED=∠CFD=90°,∴∠EDB=∠FDC=30°,
∵DE=m,DF=n,且3m=4n和m2+n2=25,
∴m=
| 4n |
| 3 |
∴(
| 4n |
| 3 |
解得:n=3,则m=4,
∴DE=4,DF=3,
∵cos30°=
| ED |
| BD |
∴BD=
| ED |
| cos30° |
| 4 | ||||
|
8
| ||
| 3 |
∵cos30°=
| DF |
| DC |
∴CD=
| DF |
| cos30° |
| 3 |
∴BC=
8
| ||
| 3 |
| 3 |
14
| ||
| 3 |
则AB的长为
| 14 |
| 3 |
| 3 |
点评:此题考查了等边三角形的性质与判定以及一元二次方程根的判别式、锐角三角函数关系等知识,解题的关键是求出BD,CD的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
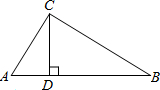 (2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( )
(2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( )