题目内容
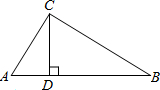 (2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( )
(2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( )分析:先利用根与系数的关系得到AC+BC=4和AC•BC=2,再把AC+BC=4两边平方,得到AC2+BC2的值,由勾股定理可得AB2=AC2+BC2,从而求出斜边AB的值,又因为S△ABC=
AC•BC=
AB×CD,所以把已知数据代入可求出CD的长.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,
∴AC+BC=-
=4,AC•BC=
=2,
∴(AC+BC)2=16,
∴AC2+BC2+2AC•BC=16,
∴AC2+BC2=16-2AC•BC=12,
∵∠C=90°,
∴AB2=AC2+BC2=12,
∴AB=
=2
,
∵S△ABC=
AC•BC=
AB×CD,
∴
×2=
×2
×CD,
∴CD=
.
故选A.
∴AC+BC=-
| b |
| a |
| c |
| a |
∴(AC+BC)2=16,
∴AC2+BC2+2AC•BC=16,
∴AC2+BC2=16-2AC•BC=12,
∵∠C=90°,
∴AB2=AC2+BC2=12,
∴AB=
| 12 |
| 3 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴CD=
| ||
| 3 |
故选A.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
和勾股定理以及三角形的面积公式的应用.
| b |
| a |
| c |
| a |

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目