Question

【题目】如图所示，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=60°，∠C=70°，求∠DAE、∠BOA的度数．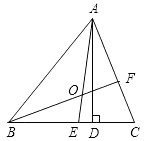

Answer 1

【答案】解∵AD⊥BC， ∴∠ADC=90°，
∵∠C=70°，
∴∠CAD=180°﹣90°﹣70°=20°，
∵∠BAC=60°，AE是∠BAC的角平分线，
∴∠EAC=∠BAE=30°，
∴∠EAD=∠EAC﹣∠CAD=30°﹣20°=10°，
∠ABC=180°﹣∠BAC﹣∠C=50°，
∵BF是∠ABC的角平分线，
∴∠ABO=25°，
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°．
故∠DAE，∠BOA的度数分别是10°，125°
【解析】根据垂直的定义、角平分线的定义、三角形内角和定理计算即可．