��Ŀ����
����Ŀ�������������
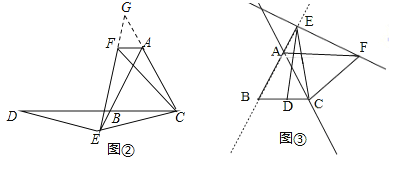
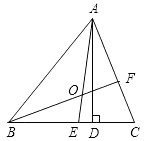
��ͼ�٣���֪��ABC�ǵ��������Σ���E���߶�AB�ϣ���D��ֱ��BC�ϣ���ED=EC������BCE�Ƶ�C˳ʱ����ת60������ACF����EF����֤����AB=DB+AF��
�����̽����
��1����ͼ�ڣ������E���߶�AB���ӳ����ϣ������������䣬�߶�AB��DB��AF֮������������������ϵ����˵��������
��2�������E���߶�BA���ӳ����ϣ������������䣬����ͼ�۵Ļ����Ͻ�ͼ�β�����������д��AB��DB��AF֮���������ϵ������˵�����ɣ�

���𰸡������������֤������������������̽������1��AB=BD+AF����2��AF=AB+BD��
��������
��������������жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬������EAF=��BAC+��CAF=120�㣬��DBE=120�㣬��EAF=��DBE��Ȼ�����ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��AB=AE+BF������AB=DB+AF��
��1�������жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬������EFC=��FGC+��FCG����BAC=��FGC+��FEA����FCG=��FEA���ٸ�����FCG=��EAD����D=��EAD���ɵ���D=��FEA��Ȼ�����ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��EB=AF�������жϳ�AB=BD��AF���ɣ�
��2�����ȸ��ݵ�E���߶�BA���ӳ����ϣ���ͼ�۵Ļ����Ͻ�ͼ�β���������Ȼ���жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬���жϳ���DBE=��EAF����BDE=��AEF��������ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��EB=AF�������жϳ�AF=AB+BD���ɣ�
���������ED=EC=CF���ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF�����ECF=60�㣬��BCA=60�㣬BE=AF��EC=CF�����CEF�ǵȱ������Σ���EF=EC����CEF=60�㣬����ED=EC����ED=EF���ߡ�ABC�ǵ��������Σ���BCA=60�㣬���ABC�ǵȱ������Σ����CAF=��CBA=60�㣬���EAF=��BAC+��CAF=120�㣬��DBE=120�㣬��EAF=��DBE���ߡ�CAF=��CEF=60�㣬��A��E��C��F�ĵ㹲Բ�����AEF=��ACF������ED=EC�����D=��BCE����BCE=��ACF�����D=��AEF������EDB����FEA�У��ߡ�DBE=��EAF����D=��AEF��ED=EF��AAS�������EDB�ա�FEA����DB=AE��BE=AF����AB=AE+BE����AB=DB+AF��
��1��AB=BD+AF��
�ӳ�EF��CA���ڵ�G���ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF�����ECF=60�㣬BE=AF��EC=CF�����CEF�ǵȱ������Σ���EF=EC������ED=EC����ED=EF����EFC=��BAC=60�㣬�ߡ�EFC=��FGC+��FCG����BAC=��FGC+��FEA�����FCG=��FEA�����ߡ�FCG=��ECD����D=��ECD�����D=��FEA������ת�����ʣ��ɵ���CBE=��CAF=120�㣬���DBE=��FAE=60�㣬����EDB����FEA�У��ߡ�DBE=��EAF����D=��AEF��ED=EF��AAS�������EDB�ա�FEA����BD=AE��EB=AF����BD=FA+AB����AB=BD��AF��
��2����ͼ�ۣ���ED=EC=CF���ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF�����ECF=60�㣬BE=AF��EC=CF��BC=AC�����CEF�ǵȱ������Σ���EF=EC������ED=EC����ED=EF����AB=AC��BC=AC�����ABC�ǵȱ������Σ����ABC=60�㣬���ߡ�CBE=��CAF�����CAF=60�㣬���EAF=180�㩁��CAF����BAC=180�㩁60�㩁60��=60�����DBE=��EAF����ED=EC�����ECD=��EDC�����BDE=��ECD+��DEC=��EDC+��DEC�����ߡ�EDC=��EBC+��BED�����BDE=��EBC+��BED+��DEC=60��+��BEC���ߡ�AEF=��CEF+��BEC=60��+��BEC�����BDE=��AEF������EDB����FEA�У��ߡ�DBE=��EAF����BDE=��AEF��ED=EF��AAS�������EDB�ա�FEA����BD=AE��EB=AF����BE=AB+AE����AF=AB+BD����AB��DB��AF֮���������ϵ�ǣ�AF=AB+BD��