ĢāÄæÄŚČŻ
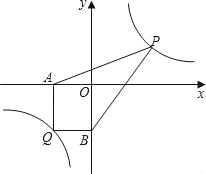
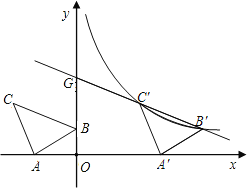
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠÓŠRt”÷ABC£¬”ĻA£½90”ć£¬AB£½AC£¬A£Ø£2£¬0£©”¢
B£Ø0£¬1£©”¢C£Ød£¬2£©”£
£Ø1£©ĒódµÄÖµ£»
£Ø2£©½«”÷ABCŃŲxÖįµÄÕż·½ĻņĘ½ŅĘ£¬ŌŚµŚŅ»ĻóĻŽÄŚB”¢CĮ½µćµÄ¶ŌÓ¦µćB”䔢C”äÕżŗĆĀäŌŚÄ³·“±ČĄżŗÆŹżĶ¼
ĻńÉĻ”£ĒėĒó³öÕāøö·“±ČĄżŗÆŹżŗĶ“ĖŹ±µÄÖ±ĻßB”äC”äµÄ½āĪöŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Ö±ĻßB”äC”ä½»yÖįÓŚµćG”£ĪŹŹĒ·ń“ęŌŚxÖįÉĻµÄµćMŗĶ·“±ČĄżŗÆŹżĶ¼ĻńÉĻµÄµćP£¬
Ź¹µĆĖıߊĪPGMC”äŹĒĘ½ŠŠĖıߊĪ”£Čē¹ū“ęŌŚ£¬ĒėĒó³öµćMŗĶµćPµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ”£
”¾“š°ø”æ£Ø1£©-3£Ø2£©![]() £¬
£¬![]() £Ø3£©P”ä£Ø
£Ø3£©P”ä£Ø![]() £¬5£©£¬M”ä£Ø
£¬5£©£¬M”ä£Ø![]() £¬0£©£¬ŌņµćP”äĪŖĖłĒóµÄµćP£¬µćM”äĪŖĖłĒóµÄµćM”£
£¬0£©£¬ŌņµćP”äĪŖĖłĒóµÄµćP£¬µćM”äĪŖĖłĒóµÄµćM”£
”¾½āĪö”æ
½ā£ŗ£Ø1£©×÷CN”ĶxÖįÓŚµćN”£
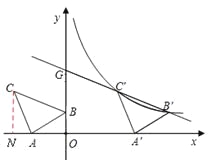
ŌŚRt”÷CNAŗĶRt”÷AOBÖŠ£¬
”ßNC£½OA£½2£¬AC£½AB
”ąRt”÷CNA”ÕRt”÷AOB£ØHL£©”£
”ąAN£½BO£½1£¬NO£½NA£«AO£½3£¬
Ó֔ߵćCŌŚµŚ¶žĻóĻŽ£¬”ąd£½£3”£
£Ø2£©Éč·“±ČĄżŗÆŹżĪŖ![]() £¬µćC”äŗĶB”äŌŚøƱȥżŗÆŹżĶ¼ĻńÉĻ£¬
£¬µćC”äŗĶB”äŌŚøƱȥżŗÆŹżĶ¼ĻńÉĻ£¬
ÉčC”ä£Øc£¬2£©£¬ŌņB”ä£Øc£«3£¬1£©”£
°ŃµćC”äŗĶ£Ā”äµÄ×ų±ź·Ö±š“śČė![]() £¬µĆk£½2 c£»k£½c£«3”£
£¬µĆk£½2 c£»k£½c£«3”£
”ą2 c£½c£«3£¬c£½3£¬Ōņk£½6”£”ą·“±ČĄżŗÆŹż½āĪöŹ½ĪŖ![]() ”£
ӣ
µĆµćC”ä£Ø3£¬2£©£»B”ä£Ø6£¬1£©”£
ÉčÖ±ĻßC”äB”äµÄ½āĪöŹ½ĪŖy£½ax£«b£¬°ŃC”䔢B”äĮ½µć×ų±ź“śČėµĆ![]() £¬½āµĆ
£¬½āµĆ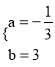 ”£
ӣ
”ąÖ±ĻßC”äB”äµÄ½āĪöŹ½ĪŖ![]() ”£
ӣ
£Ø3£©ÉčQŹĒG C”äµÄÖŠµć£¬ÓÉG£Ø0£¬3£©£¬C”ä£Ø3£¬2£©£¬µĆµćQµÄŗį×ų±źĪŖ![]() £¬µćQµÄׯ×ų±źĪŖ
£¬µćQµÄׯ×ų±źĪŖ
2£«![]() ”£”ąQ£Ø
”£”ąQ£Ø![]() £¬
£¬![]() £©”£
£©”£
¹żµćQ×÷Ö±ĻßlÓėxÖį½»ÓŚM”äµć£¬
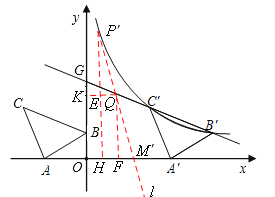
Óė![]() µÄĶ¼Ļó½»ÓŚP”äµć£¬ČōĖıߊĪP”äG M”ä C”äŹĒĘ½ŠŠĖıߊĪ£¬ŌņÓŠP”äQ£½Q M”䣬Ņ×ÖŖµćM”äµÄŗį×ų±ź“óÓŚ
µÄĶ¼Ļó½»ÓŚP”äµć£¬ČōĖıߊĪP”äG M”ä C”äŹĒĘ½ŠŠĖıߊĪ£¬ŌņÓŠP”äQ£½Q M”䣬Ņ×ÖŖµćM”äµÄŗį×ų±ź“óÓŚ![]() £¬µćP”äµÄŗį×ų±źŠ”ÓŚ
£¬µćP”äµÄŗį×ų±źŠ”ÓŚ![]() ”£
ӣ
×÷P”ä£Č”ĶxÖįÓŚµćH£¬QK”ĶyÖįÓŚµćK£¬P”äHÓėQK½»ÓŚµćE£¬×÷QF”ĶxÖįÓŚµćF£¬
Ōņ”÷P”äEQ”Õ”÷QFM”ä ”£
ÉčEQ£½FM”䣽t£¬ŌņµćP”äµÄŗį×ų±źxĪŖ![]() £¬µćP”äµÄׯ×ų±źyĪŖ
£¬µćP”äµÄׯ×ų±źyĪŖ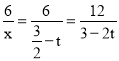 £¬
£¬
µćM”äµÄ×ų±źŹĒ£Ø![]() £¬0£©”£
£¬0£©”£
”ąP”äE£½![]() ”£
ӣ
ÓÉP”äQ£½QM”䣬µĆP”äE2£«EQ2£½QF2£«FM”ä2£¬”ą![]() £¬
£¬
ÕūĄķµĆ£ŗ![]() £¬½āµĆ
£¬½āµĆ![]() £Ø¾¼ģŃ飬ĖüŹĒ·ÖŹ½·½³ĢµÄ½ā£©”£
£Ø¾¼ģŃ飬ĖüŹĒ·ÖŹ½·½³ĢµÄ½ā£©”£
”ą![]() £¬
£¬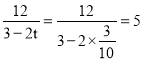 £¬
£¬![]() ”£
ӣ
”ąP”ä£Ø![]() £¬5£©£¬M”ä£Ø
£¬5£©£¬M”ä£Ø![]() £¬0£©£¬ŌņµćP”äĪŖĖłĒóµÄµćP£¬µćM”äĪŖĖłĒóµÄµćM”£
£¬0£©£¬ŌņµćP”äĪŖĖłĒóµÄµćP£¬µćM”äĪŖĖłĒóµÄµćM”£
£Ø1£©×÷CN”ĶxÖįÓŚµćN£¬ÓÉRt”÷CNA”ÕRt”÷AOB¼“æÉĒóµĆdµÄÖµ”£
£Ø2£©øł¾ŻĘ½ŅʵĊŌÖŹ£¬ÓĆ“ż¶ØĻµŹż·ØĒó³ö·“±ČĄżŗÆŹżŗĶÖ±ĻßB”äC”äµÄ½āĪöŹ½”£
£Ø3£©øł¾ŻĘ½ŠŠĖıߊĪ¶Ō½ĒĻß»„ĻąĘ½·ÖµÄŠŌÖŹ£¬Č”G C”äµÄÖŠµćQ£¬¹żµćQ×÷Ö±ĻßlÓėxÖį½»ÓŚM”äµć£¬Óė![]() µÄĶ¼Ļó½»ÓŚP”äµć£¬Ēó³öP”äQ£½Q M”äµÄµćM”äŗĶP”äµÄ×ų±ź¼“æÉ”£
µÄĶ¼Ļó½»ÓŚP”äµć£¬Ēó³öP”äQ£½Q M”äµÄµćM”äŗĶP”äµÄ×ų±ź¼“æÉ”£

 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø”¾ĢāÄæ”æÄĻ¹ūĄęŹĒ¶«±±ĮÉÄžŹ”µÄŅ»“óĢŲ²ś£¬ĻÖÓŠ20æšÄĻ¹śĄę£¬ŅŌĆææš25Ē§æĖĪŖ±ź×¼£¬³¬¹ż»ņ²»×ćµÄĒ§æĖŹż·Ö±šÓĆÕż”¢øŗŹżĄ“±ķŹ¾£¬¼ĒĀ¼ČēĻĀ£ŗ
Óė±ź×¼ÖŹĮæµÄ²īÖµ £Øµ„Ī»£ŗĒ§æĖ£© | £3 | £2 | £1.5 | 0 | 1 | 2.5 |
æšŹż | 1 | 4 | 2 | 3 | 2 | 8 |
£Ø1£©20æšÄĻ¹ūĄęÖŠ£¬×īÖŲµÄŅ»æš±Č×īĒįµÄŅ»æšÖŲ¶ąÉŁĒ§æĖ£æ
£Ø2£©Óė±ź×¼ÖŲĮæ±Č½Ļ£¬20æšÄĻ¹ūĄę×Ü¼Ę³¬¹ż»ņ²»×涹ɣĒ§æĖ£æ
£Ø3£©ČōÄĻ¹ūĄęĆæĒ§æĖŹŪ¼Ū4ŌŖ£¬ŌņÕā20æšæÉĀō¶ąÉŁŌŖ£æ