Question

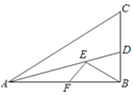
【题目】如图，在Rt△ABC中，AC=6，AB=，∠BAC=30°，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，则BE+EF的最小值是_____．

Answer 1

【答案】

【解析】

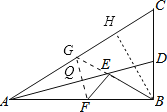
作FG⊥AD交AC于点G，交AD于点Q，作BH⊥AC，连接EG，由AD是角平分线可得∠BAD=∠CAD，利用ASA可证明△AQG≌△AQF，可得AF=AG，利用SAS可证明△AEF≌△AEG，可得EG=EF，即可求得BE+EF=BG，根据BG最短为BH，即可得答案.

作FG⊥AD交AC于点G，交AD于点Q，作BH⊥AC，连接EG，

∵AD平分∠BAC，

∴∠BAD=∠CAD，

在△AQG和△AQF中，，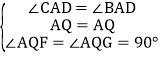

∴△AQG≌△AQF（ASA），

∴AF=AG，

在△AEF和△AEG中，，

∴△AEF≌△AEG（SAS），

∴EG=EF，

∴BE+EF=BE+EG=BG，

∵BG最短为BH，

∴BE+EF最短为BH，

∵AB=，∠BAC=30°，

∴BH=AB=，

故答案为：