题目内容
【题目】如图，在矩形ABCD中，AB=6，BC=8，点M，N同时从点B出发，分别在BC，BA上运动，若点M的运动速度是每秒2个单位长度，且是点N运动速度的2倍，当其中一个点到达终点时，停止一切运动．以MN为对称轴作△MNB的对称图形△MNB1．点B1恰好在AD上的时间为______秒．在整个运动过程中，△MNB1与矩形ABCD重叠部分面积的最大值为______．
【答案】
【解析】
（1）如图，当B′与AD交于点E，作FM⊥AD于F，根据轴对称的性质可以得出ME=MB=2t，由勾股定理就可以表示出EF，就可以表示出AE，再由勾股定理就可以求出t的值；
（2）根据三角形的面积公式，分情况讨论，当0＜t≤和＜t≤4时由求分段函数的方法就可以求出结论．
（1）如下图，当B′与AD交于点E，作FM⊥AD于F．
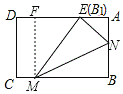
∴∠DFM=90°．
∵四边形ABCD是矩形，
∴CD=AB．AD=BC．∠D=∠C=90°．
∴四边形DCMF是矩形，
∴CD=MF．
∵△MNB与△MNE关于MN对称，
∴△MNB≌△MNE，
∴ME=MB，NE=BN．
∵BN=t，BM=2t，
∴EN=t，ME=2t．
∵AB=6，BC=8，
∴CD=MF=6，CB=DA=8．AN=6-t
在Rt△MEF和Rt△AEN中，由勾股定理，得
EF=
，AE=
，
∴+=2t，
∴t=．
（2）如图所示：
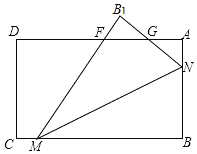
∵△MNB1与△MNB关于MN对称，
∴∠MB1N=∠MBN=90°．
∵∠MB1N+∠MBN+∠B1MB+∠B1NB=360°，
∴∠B1MB+∠B1NB=180°．
∵∠B1NA+∠B1NB=180°，
∴∠B1NA=∠B1MB．
在变化过程中
,∴∠B1NA不变
由（1）得tan∠B1NA=
，
∴tan∠B1MB=．
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠B1FG=∠B1MB．
∵BN=t，BM=2t，
∴B1N=t，MB1=2t．
∵AB=6，BC=8，
∴CD=MF=6，CB=DA=8．AN=6-t
∴GA=（6-t），GN=
（6-t），
∵B1G=B1N-GN=t-（6-t）=
t-10，
∴B1F=（t-10）×
=2t-
．
∴当＜t≤4时，
S=t2-
（2t-）（t-10）=-（t-6）2+
，
∴t=4时，S最大=．
当0＜t≤时，S=t2．
∴t=时，S最大=
．
∵＞．
∴最大值为．
故答案为：（1）；（2）．
