题目内容
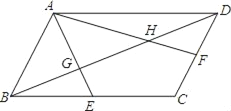
【题目】如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
因为四边形ABCD是平行四边形,所以AD∥BC,所以△AGD∽△EGB,由相似三角形的性质和已知条件可得:BG:GD=BE:AD=1:2,同理可证明△AHB∽FHD,由相似的性质可得:DH:HB=DF:AB=1:2,即G,H是BD三等分点,所以![]() 又因为S△ABE=
又因为S△ABE=![]() S平行四边形ABCD,所以S平行四边形ABCD
S平行四边形ABCD,所以S平行四边形ABCD![]() 即可求解.
即可求解.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AGD∽△EGB,
∵E,F分别是平行四边形ABCD边BC,CD中点,
∴BG:GD=BE:AD=1:2,
同理△AHB∽FHD,
∴DH:HB=DF:AB=1:2,
∴![]()
同理:![]()
∴BG=DH=GH,
即G,H是BD三等分点,
∴![]()
∵AH:HF=2:1,
∴AG:GE=2:1,
∴![]()
又∵S△ABE=![]() S平行四边形ABCD,
S平行四边形ABCD,
∴S平行四边形ABCD![]()
![]()
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目