题目内容
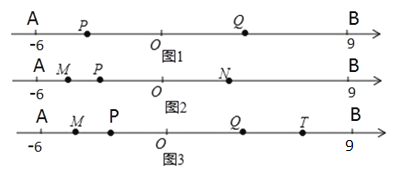
【题目】点![]() 在直线
在直线![]() 上,射线
上,射线![]() 在直线
在直线![]() 的上方,且
的上方,且![]()
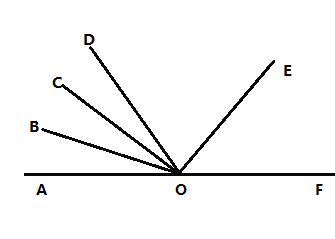
(1)如图1,![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]()
①若![]() =
=![]() ,则
,则![]() = .
= .
②若![]() =
=![]() ,则
,则![]() = .
= .
③若![]() =
=![]() ,则
,则![]() = °(用含
= °(用含![]() 的式子表示)
的式子表示)
(2)当![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]() 时,请画出图形;此时,
时,请画出图形;此时,![]() 与
与![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
【答案】(1)①40°;②25°;③(80-2n);(2)作图见详解;∠EOF=80°+2∠COD.
【解析】
(1)①由题意利用角平分线的定义和邻补角相加等于180°进行分析即可;
②根据题意设∠COD=x°,并利用角平分线的定义和邻补角相加等于180答题即可;
③根据题意可知需要利用角平分线的定义和邻补角相加等于180°来进行分析;
(2)根据题意画出新图形,并由题意用代数式分别表示∠COD与∠EOF,进而得出数量关系式.
解:(1)①∵∠AOB=40°,∠AOC=70°
∴∠BOC=30°
∵∠COD=20°
∴∠BOD=∠BOC+∠COD=50°
∵OD平分∠BOE
∴∠DOE=∠BOD=50°
∴∠EOF=180°-∠AOB-∠DOE-∠BOD=40°.
②设∠COD=x°,则由上题可知:
∠BOD=∠DOE=30°+x°
∴∠EOF=180°-(∠AOC+∠COD+∠DOE)=30°
∴∠COD=25°
③由上题可知:
∠BOD=∠DOE=30°+n°
∴∠EOF=180°-(∠AOC+∠COD+∠DOE)=180°-(70°+n°+30°+n°)=80°-2n°
故答案为①40°;②25°;③(80-2n).
(2)作图如下:
∠COD与∠EOF的数量关系是:∠EOF=80°+2∠COD,理由如下:
∵∠AOC=70°
∴∠COF=110°
∴∠EOF=∠EOC+110°
∵∠COD=∠EOC+∠DOE,①
∠DOE= ![]() ,
,
∴∠COD=15°+ ![]() ∠EOC,②
∠EOC,②
∴由①②得:∠EOF=80°+2∠COD.
答:∠COD与∠EOF的数量关系是:∠EOF=80°+2∠COD.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案