ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ![]() Θ§“―÷Σ‘Ύ ΐ÷α…œ”–
Θ§“―÷Σ‘Ύ ΐ÷α…œ”–![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§Βψ
ΝΫΒψΘ§Βψ![]() ±μ ΨΒΡ ΐ «
±μ ΨΒΡ ΐ «![]() Θ§Βψ
Θ§Βψ![]() ±μ ΨΒΡ ΐ «
±μ ΨΒΡ ΐ «![]() Θ°Βψ
Θ°Βψ![]() ‘Ύ ΐ÷α…œ¥”Βψ
‘Ύ ΐ÷α…œ¥”Βψ![]() ≥ωΖΔΘ§“‘ΟΩΟκ
≥ωΖΔΘ§“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»―Ί ΐ÷α’ΐΖΫœρ‘ΥΕ·Θ§Ά§ ±Θ§Βψ
ΗωΒΞΈΜΒΡΥΌΕ»―Ί ΐ÷α’ΐΖΫœρ‘ΥΕ·Θ§Ά§ ±Θ§Βψ![]() ‘Ύ ΐ÷α…œ¥”Βψ
‘Ύ ΐ÷α…œ¥”Βψ![]() ≥ωΖΔΘ§“‘ΟΩΟκ
≥ωΖΔΘ§“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»‘Ύ―Ί ΐ÷αΗΚΖΫœρ‘ΥΕ·Θ§Β±Βψ
ΗωΒΞΈΜΒΡΥΌΕ»‘Ύ―Ί ΐ÷αΗΚΖΫœρ‘ΥΕ·Θ§Β±Βψ![]() ΒΫ¥οΒψ
ΒΫ¥οΒψ![]() ±Θ§ΝΫΒψΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ°…η‘ΥΕ· ±ΦδΈΣ
±Θ§ΝΫΒψΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ°…η‘ΥΕ· ±ΦδΈΣ![]() ΟκΘ°
ΟκΘ°
Θ®1Θ©![]() _______ΘΜ
_______ΘΜ![]() ±Θ§Βψ
±Θ§Βψ![]() ±μ ΨΒΡ ΐ «_______ΘΜΒ±
±μ ΨΒΡ ΐ «_______ΘΜΒ±![]() _______ ±Θ§
_______ ±Θ§![]() ΓΔ
ΓΔ![]() ΝΫΒψœύ”ωΘΜ
ΝΫΒψœύ”ωΘΜ
Θ®2Θ©»γΆΦ![]() Θ§»τΒψ
Θ§»τΒψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ΒΡ÷–ΒψΘ§Βψ
ΒΡ÷–ΒψΘ§Βψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ÷–ΒψΘ§Βψ
÷–ΒψΘ§Βψ![]() ‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§œΏΕΈ
‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§œΏΕΈ![]() ΒΡ≥ΛΕ» «ΖώΖΔ…ζ±δΜ·ΘΩ»τ±δΜ·Θ§«κΥΒΟςάμ”…ΘΜ»τ≤Μ±δΘ§«κ«σ≥ωœΏΕΈ
ΒΡ≥ΛΕ» «ΖώΖΔ…ζ±δΜ·ΘΩ»τ±δΜ·Θ§«κΥΒΟςάμ”…ΘΜ»τ≤Μ±δΘ§«κ«σ≥ωœΏΕΈ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
Θ®3Θ©»γΆΦ![]() Θ§»τΒψ
Θ§»τΒψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ΒΡ÷–ΒψΘ°Βψ
ΒΡ÷–ΒψΘ°Βψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ÷–ΒψΘ§‘ρ÷±Ϋ”–¥≥ω”ΟΚ§
÷–ΒψΘ§‘ρ÷±Ϋ”–¥≥ω”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΒΡœΏΕΈ
ΒΡ¥ζ ΐ Ϋ±μ ΨΒΡœΏΕΈ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©15ΘΜ![]() ΘΜ3ΘΜΘ®2Θ©≤Μ±δΜ·Θ§
ΘΜ3ΘΜΘ®2Θ©≤Μ±δΜ·Θ§![]() =7.5ΘΜΘ®3Θ©
=7.5ΘΜΘ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
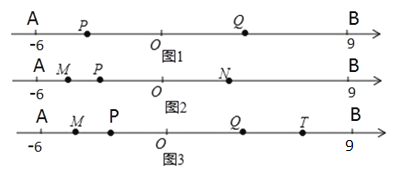
Θ®1Θ©ΗυΨίΝΫΒψΦδΨύάκΒΡΕ®“εΘ§œΏΕΈΒΡΚΆ≤νΕ®“εΦΤΥψΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίœΏΕΈΒΡ÷–ΒψΕ®“εΘ§Ω…ΒΟMN=MP+NP= ![]() Θ®AP+BPΘ©=
Θ®AP+BPΘ©= ![]() ABΘΜ
ABΘΜ
Θ®3Θ©”…Χβ“βΗυΨίœΏΕΈΒΡ÷–ΒψΕ®“εΘ§œΏΕΈΚΆ≤νΕ®“εΦΤΥψΦ¥Ω….
ΫβΘΚΘ®1Θ©AB=9-Θ®-6Θ©=15Θ§
t=1 ±Θ§BQ=3Θ§OQ=6Θ§
…ηtΟκΚσœύ”ωΘ§”…Χβ“βΘ®2+3Θ©t=15Θ§t=3Θ§
Ι ¥πΑΗΈΣΘΚ15Θ§6Θ§3.
Θ®2Θ©¥πΘΚMN≥ΛΕ»≤Μ±δΘ§άμ”…»γœ¬ΘΚ
ΓΏMΈΣAP÷–ΒψΘ§NΈΣBP÷–Βψ
ΓύMP=![]() APΘ§NP=
APȧNP=![]() BPȧ
BPȧ
ΓύMN=MP+NP=![]() Θ®AP+BPΘ©=
Θ®AP+BPΘ©=![]() AB=7.5Θ°
AB=7.5Θ°
Θ®3Θ©ΗυΨίΧβ“βΖ÷±πΒΟΒΫΒψM±μ ΨΒΡ ΐΈΣt-6ΘΜΒψT±μ ΨΒΡ ΐΈΣ9-1.5tΘΜ
ΗυΨίΝΫΒψΦδΨύάκΒΡΕ®“εΩ…ΒΟMT= 9-1.5t-Θ®t-6Θ©=15-2.5t.
Ι ¥πΑΗΈΣΘΚ![]() .
.