题目内容
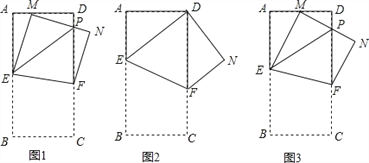
【题目】如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
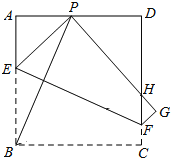
(1)求证:∠APB=∠BPH;
(2)若P为AD中点,求四边形EFGP的面积;
(3)当点P在边AD上移动时,△PDH的周长是否发生变化?写出你的结论并证明.
【答案】(1)见解析;(3)![]() ;(3)△PHD的周长不变为定值12,见解析.
;(3)△PHD的周长不变为定值12,见解析.
【解析】
(1)欲证明∠APB=∠BPH,只要证明∠APB+∠EBP=90°,∠BPH+∠EPB=90°,根据EP=EB,推出∠EBP=∠EPB即可证明.
(2)如图1中,作FM⊥AB于M.由△ABP≌△MFE,推出AP=EM=3,想办法求出EB、CF即可解决问题.
(3)△PHD的周长不变为定值12.如图2中,作BQ⊥PG于Q,连接BH,分别证明△BPA≌△BPQ和△BHQ≌△BHC即可.
(1)∵PE=BE,∴∠EBP=∠EPB.
∵∠A=∠ABC=∠EPG=90°,∴∠APB+∠EBP=90°,∠BPH+∠EPB=90°,∴∠APB=∠BPH.
(2)如图1中,作FM⊥AB于M.
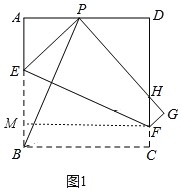
∵∠BEF+∠ABP=90°,∠BEF+∠EFM=90°,∴∠ABP=∠EFM.
在△ABP和△MFE中,∵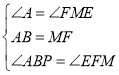 ,∴△ABP≌△MFE,∴ME=AP
,∴△ABP≌△MFE,∴ME=AP![]() AD=3.在Rt△AEP中,设AE=x,则EP=BE=6﹣x,∴(6﹣x)2=x2+32,∴x
AD=3.在Rt△AEP中,设AE=x,则EP=BE=6﹣x,∴(6﹣x)2=x2+32,∴x![]() ,∴CF=BM=AB﹣AE﹣EM
,∴CF=BM=AB﹣AE﹣EM![]() ,∴S四边形EFGP
,∴S四边形EFGP![]() (CF+BE)×BC
(CF+BE)×BC![]() (
(![]() )×6
)×6![]() .
.
(3)△PHD的周长不变为定值12.证明如下:
如图2中,作BQ⊥PG于Q,连接BH.
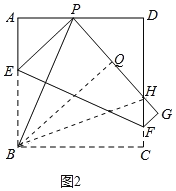
由(1)可知∠APB=∠BPQ.在△BPA和△BPQ中,∵ ,∴△BPA≌△BPQ,∴AP=PQ,AB=BQ.
,∴△BPA≌△BPQ,∴AP=PQ,AB=BQ.
∵AB=BC,∴BC=BQ.
∵∠BQH=∠C=90°,BH=BH,∴△BHQ≌△BHC,∴CH=QH,∴△PDH的周长=DP+PH+DH=(DP+AP)+(CH+DH)=AD+CD=12.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案