题目内容
【题目】如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF.求证:∠BPC=90°+![]() ∠BAC.
∠BAC.
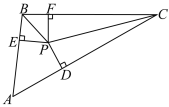
【答案】见解析.
【解析】
连接AP,且延长至G,推出点P是△ABC三角平分线的交点,求出∠CAG=∠BAG=![]() ∠BAC,∠ACP=
∠BAC,∠ACP=![]() ∠ACB,∠ABP=
∠ACB,∠ABP=![]() ∠ABC,求出∠CPG=∠PAC+∠PCA=
∠ABC,求出∠CPG=∠PAC+∠PCA=![]() (∠BAC+∠ACB),∠BPG=∠BAG+∠ABP=
(∠BAC+∠ACB),∠BPG=∠BAG+∠ABP=![]() (∠BAC+∠ABC),根据∠BPC=∠CPG+∠BPG代入求出即可.
(∠BAC+∠ABC),根据∠BPC=∠CPG+∠BPG代入求出即可.
证明:连接AP,且延长至G,
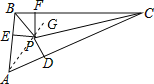
∵PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,
∴点P是△ABC三角平分线的交点,
∴AP平分∠BAC,
∴∠CAG=∠BAG=![]() ∠BAC,
∠BAC,
∵CP平分∠ACB,BP平分∠ABC,
∴∠ACP=![]() ∠ACB,∠ABP=
∠ACB,∠ABP=![]() ∠ABC,
∠ABC,
∴∠CPG=∠PAC+∠PCA=![]() (∠BAC+∠ACB),
(∠BAC+∠ACB),
∠BPG=∠BAG+∠ABP=![]() (∠BAC+∠ABC),
(∠BAC+∠ABC),
∴∠BPC=∠CPG+∠BPG
=1/2(∠BAC+∠ACB)+![]() (∠BAC+∠ABC)
(∠BAC+∠ABC)
=∠BAC+![]() (180°-∠BAC)
(180°-∠BAC)
=90°+![]() ∠BAC.
∠BAC.

【题目】近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
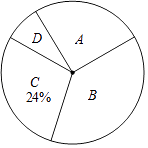
(1)表中的a=b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?





