题目内容
【题目】(1)探索发现
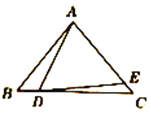
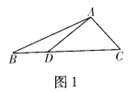
如图1,在△ABC中,点D在边BC上,△ABD与△ADC面积分别记为S1和S2,试判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(2)阅读分析
小东遇到这样一个问题:如图2,在Rt△ABC中,AB=AC,∠BAC=90°,射线AM交BC于点D,点E,F在AM上,且∠CEM=∠BFM=90°,试判断BF,CE,EF三条线段之间的数量关系.
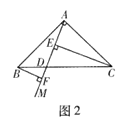
小东利用一对全等三角形,经过推理使问题得以解决.
填空:①图2中的一对全等三角形为_________;
②BF,CE,EF三条线段之间的数量关系为__________________.
(3)类比探究
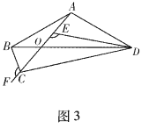
如图3,在四边形ABCD中,AB=AD,AC与BD交于点O,点E、F在射线AC上,且∠BCF=∠DEF=∠BAD.
①判断BC,DE,CE三条线段之间的数量关系,并说明理由;
②若OD=3OB,△AED的面积为2,直接写出四边形ABCD的面积.
【答案】(1)![]() =
=![]() ;(2)①△AEC≌△BFA,②EC=EF+BF; (3)①DE=BC+CE, ②8
;(2)①△AEC≌△BFA,②EC=EF+BF; (3)①DE=BC+CE, ②8
【解析】
(1)过点A作AE![]() BC,然后根据三角形面积公式求得两个三角形的面积,即可得出答案;(2)依据AAS可证明△AEC≌△BFA,由全等三角形的性质可得,AE=BF,EC=AF,由AF=EF+AE,通过等量代换即可得出答案;
BC,然后根据三角形面积公式求得两个三角形的面积,即可得出答案;(2)依据AAS可证明△AEC≌△BFA,由全等三角形的性质可得,AE=BF,EC=AF,由AF=EF+AE,通过等量代换即可得出答案;
(3)①依据AAS可证明△ABC≌△DAE,通过等量代换即可得出答案,②因为△AED的面积为2,根据全等三角形的性质可得S△ABC=2,然后根据(1)中的结论可求S△ADC=3S△ABC=6,即可得到答案.
解:(1)![]() =
=![]() ,
,
理由:如图,过点A作AE![]() BC,
BC,

∵S1=S△ABD=BD![]() AE,S2= S△ADC=DC
AE,S2= S△ADC=DC![]() AE,
AE,
∴![]() =
=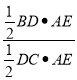 =
=![]() ;
;
(2)①△AEC≌△BFA,
理由:∵∠CEM=∠BFM=90°,
∴∠BFA=∠AEC=90°,
∴∠ABF+∠BFA=90°,
又∵∠BFA+∠FAC=90°,
∴∠ABF=∠EAC,
∵∠BFA=∠AEC=90°,
∠ABF=∠EAC,AB=AC,
∴△AEC≌△BFA.
②EC=EF+BF,
理由:∵△AEC≌△BFA,
∴AE=BF,EC=AF,
又∵AF=EF+AE,
∴EC=EF+BF.
(3)①DE=BC+CE,
理由:∵∠BCF=∠DEF,
∴∠AED=∠BCA,
∵∠ADE+∠EAD=∠DEF,
∠ABF+∠FAD=∠BAD,
∠DEF=∠BAD,
∴∠BAF=∠ADE,
∵∠AED=∠BCA,
∠BAC=∠ADE,AB=AD,
∴△ABC≌△DAE,
∴BC=AE,DE=AC,
又∵AC=AE+EC,
∴DE=BC+CE.
②∵△ABC≌△DAE, S△AED=2,
∴S△ABC=2,
∵OD=3OB,
∴![]() ,
,![]() ,
,
∴S△ADC=3S△ABC=6,
∴S四边形ABCD= S△ADC+ S△ABC=8.