题目内容
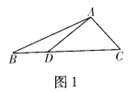
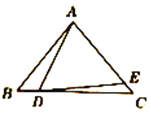
【题目】如图所示,D、E分别是△ABC的边BC、AC上的点,且AB=AC,AD=AE.
(1)若∠BAD=20°,则∠EDC= °.
(2)若∠EDC=20°,则∠BAD= °.
(3)设∠BAD=α,∠EDC=β,你能由(1)(2)中的结果找到α、β间所满足的关系吗?请说明理由.
【答案】(1)10°;(2)40°;(3)α=2β .
【解析】
问题即是弄清∠CDE与∠BAD、∠DAE、∠ADE的大小关系,通过等边对等角及外角与内角的关系探索求解.
解:(1)∵AB=AC,∴∠B=∠C,
∵AD=AE,∴∠ADE=∠AED,
又∵∠ADC=∠B+∠BAD,∠AED=∠C+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD,
即∠C+∠EDC+∠EDC=∠B+∠BAD,
∴2∠EDC=∠BAD,
∵∠BAD=20°
∴∠EDC=10;
(2) ∵AB=AC,∴∠B=∠C,
∵AD=AE,∴∠ADE=∠AED,
又∵∠ADC=∠B+∠BAD,∠AED=∠C+∠EDC,
∴∠ADE+∠EDC=∠B+∠BAD,
即∠C+∠EDC+∠EDC=∠B+∠BAD,
∴2∠EDC=∠BAD,
∵∠EDC=20°
∴∠BAD=40°
(3)设∠BAD=α,∠EDC=β,则,α=2β.
证明:∵AB=AC,
∴∠B=∠C,
又∵∠ADC=∠BAD+∠B ,
∴∠ADC=∠BAD+∠C……①,
∵AD=AE,
∴∠ADE=∠AED,
∵∠ADC=∠EDC+∠ADE,
∴∠ADC=∠EDC+∠AED,
又∵∠AED=∠EDC+∠C,
∴∠ADC=∠EDC+∠EDC+∠C=2∠EDC+∠C……②,
由①②得:∠BAD+∠C=2∠EDC+∠C,
所以:∠BAD=2∠EDC,
结论:α=2β.
故答案为(1)10°;(2)40°;(3)α=2β.

练习册系列答案
相关题目