题目内容
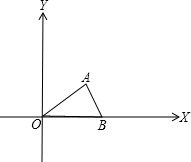
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2:1,画出△OA1B1.(所画△OA1B1与△OAB在原点两侧);
(2)求出线段A1B1所在直线的函数关系式.
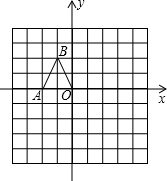
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2:1,画出△OA1B1.(所画△OA1B1与△OAB在原点两侧);
(2)求出线段A1B1所在直线的函数关系式.

(1)如图,△OA1B1就是△OAB放大后的图象.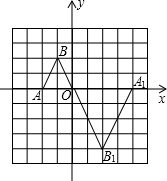
作图(3分)
则△OB1A1为所求作的三角形.
(2)由(1)可得点A1、B1的坐标分别为A1(4,0)、B1(2,-4),
故设此线的解析式为y=kx+b(k≠0),
∴
,
解得
.
故线段A1B1所在直线的函数关系式为:y=2x-8.

作图(3分)
则△OB1A1为所求作的三角形.
(2)由(1)可得点A1、B1的坐标分别为A1(4,0)、B1(2,-4),
故设此线的解析式为y=kx+b(k≠0),
∴
|
解得
|
故线段A1B1所在直线的函数关系式为:y=2x-8.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
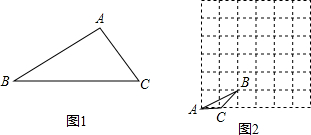 线交点处的三角形叫做格点三角形.友情提示:请在画出的三角形的项点处标上相对应的字母!)
线交点处的三角形叫做格点三角形.友情提示:请在画出的三角形的项点处标上相对应的字母!)