题目内容
【题目】某数学兴趣小组将我校九年级某班学生一分钟跳绳的测试成绩进行了整理,分成5个小组(x表成绩,单位:次,且100≤x<200),根据测试成绩绘制出部分频数分布表和部分频数分布直方图,其中B、E两组测试成绩人数直方图的高度比为4:1,请结合下列图标中相关数据回答下列问题:
测试成绩频数分布表
组别 | 成绩x次 | 频数(人数) | 频率 |
A | 100≤x<120 | 5 | |
B | 120≤x<140 | b | |
C | 140≤x<160 | 15 | 30% |
D | 160≤x<180 | 10 | |
E | 180≤x<200 | a |
(1)填空:a= ,b= ,本次跳绳测试成绩的中位数落在 组(请填写字母);
(2)补全频数分布直方图;
(3)已知本班中甲、乙两位同学的测试成绩分别为185次、195次,现要从E组中随机选取2人介绍经验,请用列表法或画树状图的方法,求出甲、乙两人中至少1人被选中的概率.

【答案】(1)a=4,b=32%,C;(2)详见解析;(3)![]() .
.
【解析】
(1)根据C的人数除以C所占的百分比,可得总人数,进而可求出A,D的所占百分比,则a,b的值可求;根据中位线的定义解答即可;
(2)由(1)中的数据即可补全频数分布直方图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙两人中至少1人被选中的情况,再利用概率公式即可求得答案.
解:(1)由题意可知总人数=15÷30%=50(人),
所以D所占百分比=10÷50×100%=20%,A所占百分比=5÷50×100%=10%,
因为B、E两组测试成绩人数直方图的高度比为4:1,
所以5a=50﹣5﹣15﹣10,
解得a=4,
所以b=16÷50×100%=32%,
因为B的人数是16人,
所以中位线落在C组,
故答案为4,32%,C;
(2)由(1)可知补全频数分布直方图如图所示:
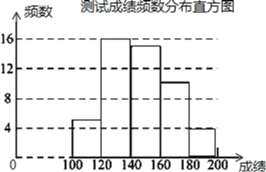
(3)设甲为A,乙为B,画树状图为:
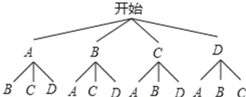
由树状图可知从E组中随机选取2人介绍经验,则甲、乙两人中至少1人被选中的概率=![]() .
.