题目内容
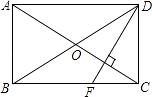
【题目】如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是( )
A.1.6
B.2.5
C.3
D.3.4
【答案】D
【解析】连接EC,由矩形的性质可得AO=CO,
又因EO⊥AC,
则由线段的垂直平分线的性质可得EC=AE,
设AE=x,则ED=AD﹣AE=5﹣x,
在Rt△EDC中,根据勾股定理可得EC2=DE2+DC2 ,
即x2=(5﹣x)2+32 ,
解得x=3.4.
故选D.
【考点精析】本题主要考查了线段垂直平分线的性质和勾股定理的概念的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?