题目内容
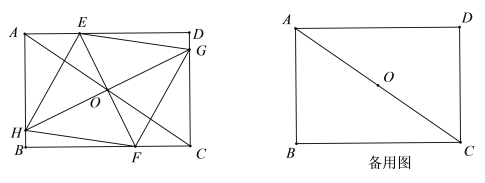
【题目】如图所示,ABCD为平行四边形,AD=13,AB=25,∠DAB=α,且cosa=![]() ,点E为直线CD上一动点,将线段EA绕点E逆时针旋转α得到线段EF,连接CF.
,点E为直线CD上一动点,将线段EA绕点E逆时针旋转α得到线段EF,连接CF.
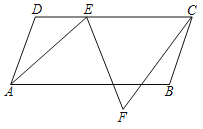
(1)求平行四边形ABCD的面积;
(2)当点C、B、F三点共线时,设EF与AB相交于点G,求线段BG的长;
(3)求线段CF的长度的最小值.
【答案】(1)300;(2) ![]() ;(3)
;(3)![]() .
.
【解析】
(1)作DK⊥AB于点K,由勾股定理求出DK,则可得出答案;
(2)延长CD至H,作∠AHD=α,过点A作AM⊥DH于点M,证明△AEH≌△EFC,得出EH=CF,CE=AH=13,证明△FBG∽△FCE,可求出BG;
(3)延长CD至P,使∠P=∠ADP=α,过点F作FM∥BC,交CD于点M,过点FN⊥CD,交CD于点N,证明△EAP≌△FEM(AAS),得出EM=AP=13,FM=EP,设DE=x,则FM=EP=10+x,CM=25-(13+x)=12-x,可用x表示FN,CN,由勾股定理求出CF,根据二次函数的性质可得出答案.
解(1)如图1,作![]() 于点
于点![]() ,
,

![]() 将线段
将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,
![]() ,且
,且![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)如图2,延长![]() 至
至![]() ,作
,作![]() ,
,

![]() ,
,
![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,
,
由(1)知![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
即![]() ,
,
![]() ;
;
(3)如图3,延长![]() 至
至![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() ,交
,交![]() 于点
于点![]() ,
,

由(2)可知![]() ,
,
在![]() 和
和![]() 中.
中.
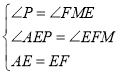 ,
,
![]() ,
,
![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
对称轴![]() ,
,
![]() 当
当![]() 时,
时,![]() 的值最小,
的值最小,![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目