Question

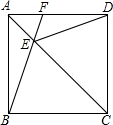在正方形ABCD中，AC为对角线，E为AC上一点，连接EB、ED．延长BE交AD于F，当∠BED=120°时，则∠EFD=

105°

．

Answer 1

分析：由四边形ABCD是正方形，易得证得△BEC≌△DEC，然后根据全等三角形的性质知对应角相等，即∠BEC=∠DEC=

1

2

∠BED，又由对顶角相等、三角形的一个内角的补角是另外两个内角的和求得∠EFD=∠BEC+∠CAD．

解答：解：∵四边形ABCD是正方形，
∴BC=CD，∠ECB=∠ECD=45°．
∴在△BEC与△DEC中，

BC=CD  ∠ECB=∠ECD  EC=EC

，
∴△BEC≌△DEC（SAS），
∴∠BEC=∠DEC=

1

2

∠BED，
∵∠BED=120°，
∴∠BEC=60°=∠AEF，
∴∠EFD=∠CAD+∠AEF=60°+45°=105°．
故答案为：105°．

点评：此题考查了正方形的性质、全等三角形的判定与性质以及三角形外角的性质．此题难度不大，注意掌握数形结合思想的应用．