题目内容
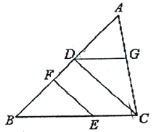
【题目】如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于 6,△BEF的面积等于4,则四边形CDFE的面积等于___________

【答案】11
【解析】
利用三角形面积公式得到AF:FE=3:2,再根据平行四边形的性质得到AD∥BE,S△ABD=S△CBD,则可判断△AFD∽△EFB,利用相似的性质可计算出S△AFD=9,所以S△ABD=S△CBD=15,然后用△BCD的面积减去△BEF的面积得到四边形CDFE的面积.
解:∵△ABF的面积等于6,△BEF的面积等于4,
即S△ABF:S△BEF=6:4=3:2,
∴AF:FE=3:2,
∵四边形ABCD为平行四边形,
∴AD∥BE,S△ABD=S△CBD,
∴△AFD∽△EFB,
∴![]() ,
,
∴S△AFD=![]() ×4=9,
×4=9,
∴S△ABD=S△CBD=6+9=15,
∴四边形CDFE的面积=15-4=11.
故答案为11.

练习册系列答案
相关题目