题目内容
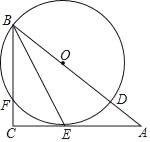
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连结DB,过点E作EM∥BD,交BA的延长线于点M。
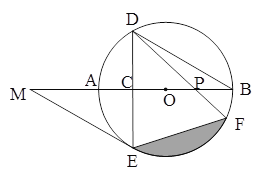
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠DPA=45°时,求图中阴影部分的面积。
【答案】(1)![]() ;(2)见证明过程:(3)
;(2)见证明过程:(3)![]()
【解析】
试题(1)连结OE,根据已知条件得出OC=![]() OE,由勾股定理可求出OE的长;
OE,由勾股定理可求出OE的长;
(2)由(1)知∠AOE=60°,![]() ,从而得出∠BDE=60°,又BD∥ME,所以∠MED=∠BDE=60°即∠MEO=90°,从而得证;
,从而得出∠BDE=60°,又BD∥ME,所以∠MED=∠BDE=60°即∠MEO=90°,从而得证;
(3)连结OF,由∠DPA=45°知∠EOF=2∠EDF=90°所以![]() ,通过计算得出结论.
,通过计算得出结论.
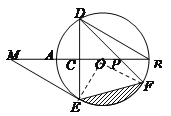
试题解析:连结OE,如图:
∵DE垂直平分半径OA
∴OC=![]() ,
,![]() ,
,
∴∠OEC=30°
∴
(2)由(1)知:∠AOE=60°,![]() ,
,
∴![]()
∴∠BDE=60°
∵BD∥ME,
∴∠MED=∠BDE=60°
∴∠MEO=90°
∴EM是⊙O的切线。
(3)连结OF
∵∠DPA=45°
∴∠EOF=2∠EDF=90°
∴![]()
考点: 1.垂径定理;2.圆周角定理;3.扇形的面积.

练习册系列答案
相关题目