题目内容
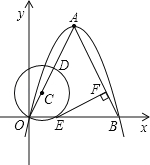
【题目】如图,已知A(2,4),以A为顶点的抛物线经过原点交x轴于B.
(1)求抛物线解析式;
(2)取OA上一点D,以OD为直径作⊙C交x轴于E,作EF⊥AB于F,求证EF是⊙C的切线;
(3)设⊙C半径为r,EF=m,求m与r的函数关系式及自变量r的取值范围;
(4)当⊙C与AB相切时,求⊙C半径r的值.
【答案】(1)y=﹣x2+4x.(2)详见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)已知了抛物线顶点的坐标,可用顶点式的二次函数通式来设二次函数的解析式,将原点的坐标代入解析式中即可求出二次函数的解析式;
(2)要证EF是圆C的切线,那么可连接CE,证CE⊥EF即可,由于EF⊥AB,那么只需证明CE∥AB即可得出EF是切线的结论,那么OC=CE,根据抛物线的对称性可得OA=AB,由这两组相等的线段即可得出∠OEC=∠ABO,由此可得证;
(3)由(2)可知∠ABO=∠AOB,那么可通过三角函数来解,根据A,O,B的坐标不难得出∠AOB,∠ABO的正弦值,那么可过C作OB的垂线,垂足为M,可在直角三角形OCM中,用∠AOB的正切值以及r的长表示出OM,也就求出了OE,进而可表示出BE的长,然后在直角三角形BFE中,根据∠ABO的正弦值用BE表示出BF,由此可得出关于m,r的函数关系式;
(4)如果⊙C与AB相切,设切点为G,那么如果连接CG,四边形CEFG就是正方形,那么r=m=EF,那么根据(3)中m,r的函数关系式,将m=r代入(3)的函数关系式中即可求出r的值.
(1)设y=a(x﹣2)2+4,由于抛物线过原点(0,0),则有0=4a+4,
即a=﹣1.
因此抛物线的解析式为:y=﹣x2+4x;
(2)连CE,
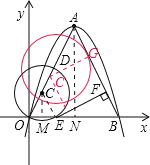
则∠COE=∠CEO,
根据A是抛物线的顶点,可知OA=AB,即∠AOB=∠OBA,
∴∠OEC=∠ABO,
∴CE∥AB,又EF⊥AB,
∴CE⊥EF,
∴EF是⊙C的切线;
(3)分别过C、A作OB的垂线,垂足分别为M、N,
直角三角形OAN中,cos∠AOB=![]() ,
,
因此:OM=![]() ,OE=2OM=
,OE=2OM=![]() ,EB=4﹣
,EB=4﹣![]() ,
,
∴![]() (0<r<
(0<r<![]() );
);
(4)设⊙C切AB于点G,
连接CG,则CG⊥AB,
∴∠CGF=∠EFG=∠CEF=90°,
∴四边形CEFG为矩形,
又CE=CG,
∴四边形CEFG为正方形,
∴EF=r,
∴m=r①,
由(3)得![]() ,
,
解得r=![]() .
.