ЬтФПФкШн
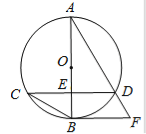
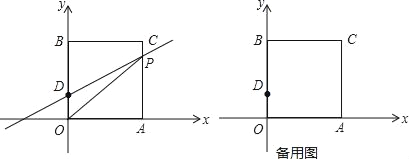
ЁОЬтФПЁПШчЭМдкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌГЄЗНаЮOACBЕФЖЅЕуAЃЌBЗжБ№дкxЃЌyжсЩЯЃЌвбжЊOAЃН3ЃЌЕуDЮЊyжсЩЯвЛЕуЃЌЦфзјБъЮЊЃЈ0ЃЌ1ЃЉЃЌCDЃН5ЃЌЕуPДгЕуAГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЯпЖЮAЉCЉBЕФЗНЯђдЫЖЏЃЌЕБЕуPгыЕуBжиКЯЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊtУы
ЃЈ1ЃЉЧѓBЃЌCСНЕузјБъЃЛ
ЃЈ2ЃЉЂйЧѓЁїOPDЕФУцЛ§SЙигкtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЕБЕуDЙигкOPЕФЖдГЦЕуEТфдкxжсЩЯЪБЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЂкЧщПіЯТЃЌжБЯпOPЩЯЧѓвЛЕуFЃЌЪЙFE+FAзюаЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЈ0ЃЌ5ЃЉЃЌCЃЈ3ЃЌ5ЃЉЃЛЃЈ2ЃЉЂйSЃНЃ![]() ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ
ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЫФБпаЮOACBЪЧОиаЮЃЌЕУЕНBCЃНOAЃН3ЃЌдкRtЁїBCDжаЃЌгЩЙДЙЩЖЈРэЕУЕНBDЃН![]() ЃН4ЃЌOBЃН5ЃЌДгЖјЧѓЕУЕуЕФзјБъЃЛ
ЃН4ЃЌOBЃН5ЃЌДгЖјЧѓЕУЕуЕФзјБъЃЛ
ЃЈ2ЃЉЂйЕБЕуPдкACЩЯЪБЃЌODЃН1ЃЌBCЃН3ЃЌSЃН![]() ЃЌЕБЕудкBCЩЯЪБЃЌODЃН1ЃЌBPЃН5+3ЉtЃН8ЉtЃЌЕУЕНSЃН
ЃЌЕБЕудкBCЩЯЪБЃЌODЃН1ЃЌBPЃН5+3ЉtЃН8ЉtЃЌЕУЕНSЃН![]() ЁС1ЁСЃЈ8ЉtЃЉЃНЉ
ЁС1ЁСЃЈ8ЉtЃЉЃНЉ![]() t+4ЃЛ
t+4ЃЛ
ЂкЕБЕуDЙигкOPЕФЖдГЦЕуТфдкxжсЩЯЪБЃЌЕУЕНЕуDЕФЖдГЦЕуЪЧЃЈ1ЃЌ0ЃЉЃЌЧѓЕУEЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉгЩЕуDЁЂEЙигкOPЖдГЦЃЌСЌНгADНЛOPгкFЃЌевЕНЕуFЃЌДгЖјШЗЖЈADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдкRtЁїAODжаЃЌгЩЙДЙЩЖЈРэЧѓЕУADЃН![]() ЃЌМДAF+EFЕФзюаЁжЕЃН
ЃЌМДAF+EFЕФзюаЁжЕЃН![]() ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉЁпЫФБпаЮOACBЪЧОиаЮЃЌ
ЁрBCЃНOAЃН3ЃЌ
дкRtЁїBCDжаЃЌЁпCDЃН5ЃЌBCЃН3ЃЌ
ЁрBDЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ЁрOBЃН5ЃЌ
ЁрBЃЈ0ЃЌ5ЃЉЃЌCЃЈ3ЃЌ5ЃЉЃЛ
ЃЈ2ЃЉЂйЕБЕуPдкACЩЯЪБЃЌODЃН1ЃЌBCЃН3ЃЌ
ЁрSЃН![]() ЃЌ
ЃЌ
ЕБЕудкBCЩЯЪБЃЌODЃН1ЃЌBPЃН5+3ЉtЃН8ЉtЃЌ
ЁрSЃН![]() ЁС1ЁСЃЈ8ЉtЃЉЃНЉ
ЁС1ЁСЃЈ8ЉtЃЉЃНЉ![]() t+4ЃЛЃЈtЁн0ЃЉ
t+4ЃЛЃЈtЁн0ЃЉ
ЂкЕБЕуDЙигкOPЕФЖдГЦЕуТфдкxжсЩЯЪБЃЌЕуDЕФЖдГЦЕуЪЧЃЈ1ЃЌ0ЃЉЃЌ
ЁрEЃЈ1ЃЌ0ЃЉЃЛ
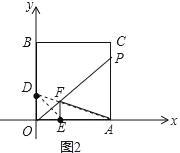
ЃЈ3ЃЉШчЭМ2ЁпЕуDЁЂEЙигкOPЖдГЦЃЌСЌНгADНЛOPгкFЃЌ
дђADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓЃЎ

ЙЪД№АИЮЊЃКЃЈ1ЃЉBЃЈ0ЃЌ5ЃЉЃЌCЃЈ3ЃЌ5ЃЉЃЛЃЈ2ЃЉЂйSЃНЃ![]() ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ
ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ