题目内容
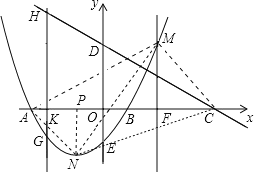
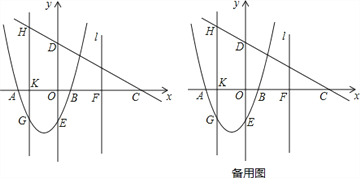
【题目】如图,抛物线y=ax2+bx-3交x轴于点A(﹣3,0),点B(1,0),交y轴于点E.点C是点A关于点B的对称点,点F是线段BC的中点,直线![]() 过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
(1)求抛物线的函数表达式;
(2)点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值;
(3)在直线![]() 上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
【答案】(1)y=x2+2x﹣3; (2)线段HG的长度有最大值![]() ; (3)当N的坐标为(﹣5,12),(11,140),(﹣1,﹣4)时,以点A、C、M、N为顶点的四边形为平行四边形.
; (3)当N的坐标为(﹣5,12),(11,140),(﹣1,﹣4)时,以点A、C、M、N为顶点的四边形为平行四边形.
【解析】试题分析:(1)把点![]() 的坐标代入函数表达式,即可求出
的坐标代入函数表达式,即可求出![]() 的值;
的值;
(2)根据C点的坐标求出直线CD的解析式,然后结合图形设出K点的坐标![]() 表达出H点和G点的坐标,列出HG关于t的表达式,根据二次函数的性质求出最大值;
表达出H点和G点的坐标,列出HG关于t的表达式,根据二次函数的性质求出最大值;
(3)需要讨论解决,①若线段AC是以点A、C,M、N为顶点的平行四边形的边,当点N在点M的左侧时,MN=3-n;当点N在点M的右侧时,MN=n-3,然后根据已知条件在求n的坐标就容易了
②若线段AC是以点A、C,M、N为顶点的平行四边形的对角线时,由“点C与点A关于点B中心对称”知:点M与点N关于点B中心对称,取点F关于点B的对称点P,则P点坐标为![]() 过P点作
过P点作![]() 轴,交抛物线于点N,结合已知条件再求n的坐标就容易了.
轴,交抛物线于点N,结合已知条件再求n的坐标就容易了.
试题解析:(1)设抛物线的函数表达式为y=a(x1)(x+3).
∵抛物线交y轴于点E(0,3),将该点坐标代入上式,得a=1,
∴所求函数表达式为y=(x1)(x+3),
即![]()
(2)∵点C是点A关于点B的对称点,点A坐标(3,0),点B坐标(1,0),
∴点C坐标(5,0),
∴将点C坐标代入![]() 得
得![]()
∴直线CD的函数表达式为![]()
设K点的坐标为(t,0),则H点的坐标为![]() G点的坐标为
G点的坐标为![]()
∵点K为线段AB上一动点,
![]()
![]()
![]()
∴当![]() 时,线段HG的长度有最大值
时,线段HG的长度有最大值![]()
(3)∵点F是线段BC的中点,点B(1,0),点C(5,0),
∴点F的坐标为(3,0),
∵直线l过点F且与y轴平行,
∴直线l的函数表达式为x=3,
∵点M在直线l上,点N在抛物线上,
∴设点M的坐标为(3,m),点N的坐标为![]()
∵点A(3,0),点C(5,0),
∴AC=8,
分情况讨论:
①若线段AC是以点A.C,M、N为顶点的平行四边形的边,则需MN![]() AC,且MN=AC=8.
AC,且MN=AC=8.
当点N在点M的左侧时,MN=3n,
∴3n=8,解得n=5,
∴N点的坐标为(5,12),
当点N在点M的右侧时,MN=n3,
∴n3=8,
解得n=11,
∴N点的坐标为(11,140),
②若线段AC是以点A.C,M、N为顶点的平行四边形的对角线,由“点C与点A关于点B中心对称”知:点M与点N关于点B中心对称,取点F关于点B的对称点P,则P点坐标为(1,0)
过P点作NP⊥x轴,交抛物线于点N,
将x=1代入![]() ,得y=4,
,得y=4,
过点N作直线NM交直线l于点M,
在△BPN和△BFM中,
∠NBP=∠MBF,
BF=BP,
![]()
∴△BPN≌△BFM,
∴NB=MB,
∴四边形ANCM为平行四边形,
∴坐标(1,4)的点N符合条件,
∴当N的坐标为(5,12),(11,140),(1,4)时,以点A. C.M、N为顶点的四边形为平行四边形.